All High School Math Resources
Example Questions
Example Question #3 : Triangles
In the figure above, what is the positive difference, in degrees, between the measures of angle ACB and angle CBD?
40
20
10
50
30
10
In the figure above, angle ADB is a right angle. Because side AC is a straight line, angle CDB must also be a right angle.
Let’s examine triangle ADB. The sum of the measures of the three angles must be 180 degrees, and we know that angle ADB must be 90 degrees, since it is a right angle. We can now set up the following equation.
x + y + 90 = 180
Subtract 90 from both sides.
x + y = 90
Next, we will look at triangle CDB. We know that angle CDB is also 90 degrees, so we will write the following equation:
y – 10 + 2x – 20 + 90 = 180
y + 2x + 60 = 180
Subtract 60 from both sides.
y + 2x = 120
We have a system of equations consisting of x + y = 90 and y + 2x = 120. We can solve this system by solving one equation in terms of x and then substituting this value into the second equation. Let’s solve for y in the equation x + y = 90.
x + y = 90
Subtract x from both sides.
y = 90 – x
Next, we can substitute 90 – x into the equation y + 2x = 120.
(90 – x) + 2x = 120
90 + x = 120
x = 120 – 90 = 30
x = 30
Since y = 90 – x, y = 90 – 30 = 60.
The question ultimately asks us to find the positive difference between the measures of ACB and CBD. The measure of ACB = 2x – 20 = 2(30) – 20 = 40 degrees. The measure of CBD = y – 10 = 60 – 10 = 50 degrees. The positive difference between 50 degrees and 40 degrees is 10.
The answer is 10.
Example Question #186 : Triangles
 If angle
If angle 


For this problem, remember that the sum of the degrees in a triangle is 
That means that 
Plug in our given values to solve:
Subtract 
Example Question #21 : Sat Mathematics
Which of the following sets of line-segment lengths can form a triangle?
In any given triangle, the sum of any two sides is greater than the third. The incorrect answers have the sum of two sides equal to the third.
Example Question #1 : How To Find An Angle In A Right Triangle
In right 



What is the value of 
24
36
30
32
48
36
There are 180 degrees in every triangle. Since this triangle is a right triangle, one of the angles measures 90 degrees.
Therefore, 
Example Question #1 : Equilateral Triangles
You are given that the perimeter of an equilateral triangle is 






By definition, an equilateral triangle has three congruent sides. The perimeter is the sum of those sides. Thus, to find the length of just one of those sides, we can divide the perimeter of the triangle by three.



Example Question #1 : Equilateral Triangles
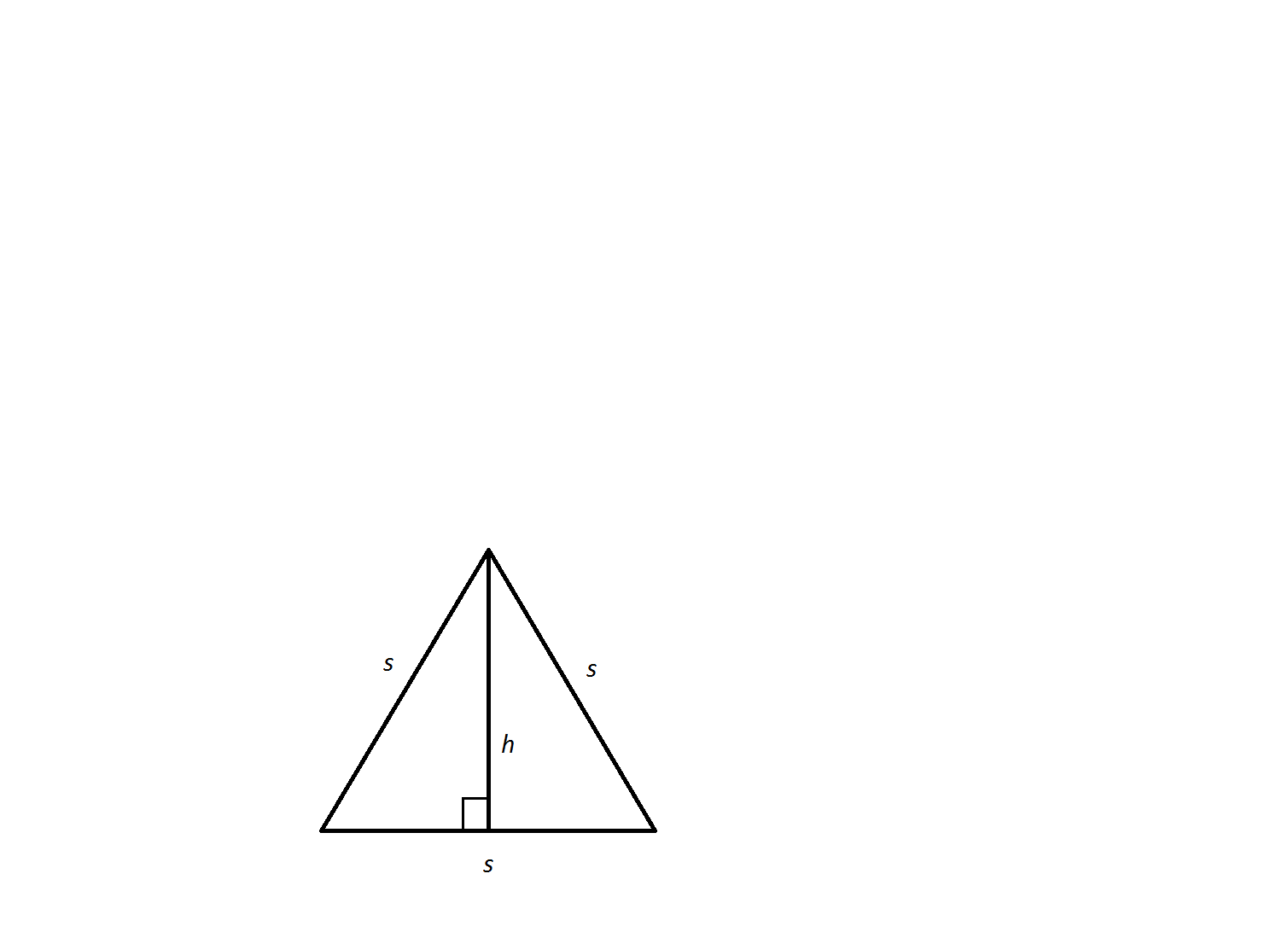
An equilateral triangle has a side length of 
Not enough information to solve
The area of an equilateral triangle is found using the following formula.

Example Question #1 : How To Find The Area Of An Equilateral Triangle
The area of square ABCD is 50% greater than the perimeter of the equilateral triangle EFG. If the area of square ABCD is equal to 45, then what is the area of EFG?
50√3
30
25√3
25
50
25√3
If the area of ABCD is equal to 45, then the perimeter of EFG is equal to x * 1.5 = 45. 45 / 1.5 = 30, so the perimeter of EFG is equal to 30. This means that each side is equal to 10.
The height of the equilateral triangle EFG creates two 30-60-90 triangles, each with a hypotenuse of 10 and a short side equal to 5. We know that the long side of 30-60-90 triangle (here the height of EFG) is equal to √3 times the short side, or 5√3.
We then apply the formula for the area of a triangle, which is 1/2 * b * h. We get 1/2 * 10 * 5√3 = 5 * 5√3 = 25√3.
In general, the height of an equilateral triangle is equal to √3 / 2 times a side of the equilateral triangle. The area of an equilateral triangle is equal to 1/2 * √3s/ 2 * s = √3s2/4.
Example Question #122 : Plane Geometry
What is the area of an equilateral triangle with sides 12 cm?
54√2
72√3
36√3
18√3
12√2
36√3
An equilateral triangle has three congruent sides and results in three congruent angles. This figure results in two special right triangles back to back: 30° – 60° – 90° giving sides of x - x √3 – 2x in general. The height of the triangle is the x √3 side. So Atriangle = 1/2 bh = 1/2 * 12 * 6√3 = 36√3 cm2.
Example Question #1 : How To Find The Area Of An Equilateral Triangle
The length of one side of an equilateral triangle is ten. What is the area of the triangle?
To calculate the height, the length of a perpendicular bisector must be determined. If a perpendicular bisector is drawn in an equilateral triangle, the triangle is divided in half, and each half is a congruent 30-60-90 right triangle. This type of triangle follows the equation below.
The length of the hypotenuse will be one side of the equilateral triangle.

The side of the equilateral triangle that represents the height of the triangle will have a length of 
To calculate the area of the triangle, multiply the base (one side of the equilateral triangle) and the height (the perpendicular bisector) and divide by two.
Example Question #3 : How To Find The Area Of An Equilateral Triangle

What is the area of an equilateral triangle with a side length of 
Not enough information to solve
In order to find the area of the triangle, we must first calculate the height of its altitude. An altitude slices an equilateral triangle into two 



Therefore, we can find the height of the altitude of this triangle by designating a value for 



Now, we can calculate the area of the triangle via the formula 
Certified Tutor
Certified Tutor
All High School Math Resources












































