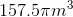Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Solid Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following polyhedron.

Ice_cream_cone

Possible Answers:

$118 \pi m^2$ $\displaystyle 118 \pi m^2$

$98 \pi m^2$ $\displaystyle 98 \pi m^2$

$88 \pi m^2$ $\displaystyle 88 \pi m^2$

$108 \pi m^2$ $\displaystyle 108 \pi m^2$

$128 \pi m^2$ $\displaystyle 128 \pi m^2$

Correct answer:

$108 \pi m^2$ $\displaystyle 108 \pi m^2$

Explanation:

The formula for the surface area of the polyhedron is:

$SA = SA_{cone}+\frac{1}{2}SA_{sphere}$ $\displaystyle SA = SA_{cone}+\frac{1}{2}SA_{sphere}$

$SA = \pi r l+\frac{1}{2}(4 \pi r^2)$ $\displaystyle SA = \pi r l+\frac{1}{2}(4 \pi r^2)$

$SA = \pi r l+2 \pi r^2$ $\displaystyle SA = \pi r l+2 \pi r^2$

Where $\displaystyle r$ is the radius of the cone, $\displaystyle l$ is the slant height of the cone, and $\displaystyle r$ is the radius of the sphere

Use the formula for a $\displaystyle 30-60-90$ triangle to find the radius and slant height:

$a-a\sqrt{2}-2a$ $\displaystyle a-a\sqrt{2}-2a$

$3\sqrt{3}m-9m-6\sqrt{3}m$ $\displaystyle 3\sqrt{3}m-9m-6\sqrt{3}m$

Plugging in our values, we get:

$SA = \pi r l+2 \pi r^2$ $\displaystyle SA = \pi r l+2 \pi r^2$

$SA = (\pi)(3\sqrt{3}m)(6\sqrt{3}m)+2(\pi)(3\sqrt{3}m)^2$ $\displaystyle SA = (\pi)(3\sqrt{3}m)(6\sqrt{3}m)+2(\pi)(3\sqrt{3}m)^2$

$SA = 54 \pi m^2 + 54 \pi m^2 = 108 \pi m^2$ $\displaystyle SA = 54 \pi m^2 + 54 \pi m^2 = 108 \pi m^2$

Report an Error

Example Question #3 : Other Polyhedrons

Find the surface area of the following polyhedron.

Dome

Possible Answers:

$81 \pi m^2$ $\displaystyle 81 \pi m^2$

$101 \pi m^2$ $\displaystyle 101 \pi m^2$

$61 \pi m^2$ $\displaystyle 61 \pi m^2$

$91 \pi m^2$ $\displaystyle 91 \pi m^2$

$71 \pi m^2$ $\displaystyle 71 \pi m^2$

Correct answer:

$81 \pi m^2$ $\displaystyle 81 \pi m^2$

Explanation:

The formula for the surface area of the polyhedron is:

$SA = (cone:no\ base)+(cylinder:one\ base)$ $\displaystyle SA = (cone:no\ base)+(cylinder:one\ base)$

$SA = \frac{1}{2}(circumference)(slant\ height)+(base)+(circumference)(height)$ $\displaystyle SA = \frac{1}{2}(circumference)(slant\ height)+(base)+(circumference)(height)$

$SA = \frac{1}{2}(2 \pi r)(h_s)+(\pi r^2)+(2 \pi r)(h)$ $\displaystyle SA = \frac{1}{2}(2 \pi r)(h_s)+(\pi r^2)+(2 \pi r)(h)$

where $\displaystyle r$ is the radius of the cone, h_s $\displaystyle h_s$ is the slant height of the cone, $\displaystyle r$ is the radius of the cylinder, and $\displaystyle h$ is the height of the cylinder.

Use the formula for a $\displaystyle 30-60-90$ triangle to find the length of the radius:

$a-a\sqrt{3}-2a$ $\displaystyle a-a\sqrt{3}-2a$

$3m-3\sqrt{3}m-6m$ $\displaystyle 3m-3\sqrt{3}m-6m$

Plugging in our values, we get:

$SA = \frac{1}{2}(2\pi (3m))(6m)+(\pi)(3m)^2+(2\pi (3m)(9m))$ $\displaystyle SA = \frac{1}{2}(2\pi (3m))(6m)+(\pi)(3m)^2+(2\pi (3m)(9m))$

$SA = 81 \pi m^2$ $\displaystyle SA = 81 \pi m^2$

Report an Error

Example Question #2 : How To Find The Surface Area Of A Polyhedron

Find the surface area of the following polyhedron.

Ice_cream_cone

Possible Answers:

$64\sqrt{2}\pi + 32 \pi m^2$ $\displaystyle 64\sqrt{2}\pi + 32 \pi m^2$

$32\sqrt{2}\pi + 32 \pi m^2$ $\displaystyle 32\sqrt{2}\pi + 32 \pi m^2$

$64\sqrt{2}\pi + 64 \pi m^2$ $\displaystyle 64\sqrt{2}\pi + 64 \pi m^2$

$32\sqrt{2}\pi + 64 \pi m^2$ $\displaystyle 32\sqrt{2}\pi + 64 \pi m^2$

Correct answer:

$32\sqrt{2}\pi + 64 \pi m^2$ $\displaystyle 32\sqrt{2}\pi + 64 \pi m^2$

Explanation:

The formula for the surface area of a polyhedron is:

$SA = (cone)+ \frac{1}{2}(sphere)$ $\displaystyle SA = (cone)+ \frac{1}{2}(sphere)$

$SA = \frac{1}{2}(2\pi r)(h_s)+ \frac{1}{2}(4\pi r^2)$ $\displaystyle SA = \frac{1}{2}(2\pi r)(h_s)+ \frac{1}{2}(4\pi r^2)$

$SA = \pi rh_s+ 2\pi r^2$ $\displaystyle SA = \pi rh_s+ 2\pi r^2$

where $\displaystyle r$ is the radius of the polyhedron and h_s $\displaystyle h_s$ is the slant height of the cone.

Use the formula for a $\displaystyle 45-45-90$ triangle to find the length of the radius:

$a-a-a\sqrt{2}$ $\displaystyle a-a-a\sqrt{2}$

$4\sqrt{2}m-4\sqrt{2}m-8m$ $\displaystyle 4\sqrt{2}m-4\sqrt{2}m-8m$

Plugging in our values, we get:

$SA = \pi (4\sqrt{2}m)(8m)+ 2\pi (4\sqrt{2}m)^2$ $\displaystyle SA = \pi (4\sqrt{2}m)(8m)+ 2\pi (4\sqrt{2}m)^2$

$SA = 32\sqrt{2}\pi + 64 \pi m^2$ $\displaystyle SA = 32\sqrt{2}\pi + 64 \pi m^2$

Report an Error

Example Question #21 : Solid Geometry

Find the volume of the following half cylinder.

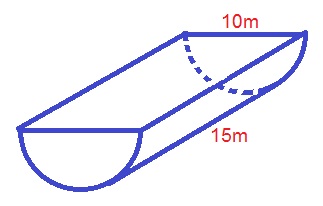
Half_cylinder

Possible Answers:

$207.5 \pi m^3$ $\displaystyle 207.5 \pi m^3$

$187.5 \pi m^3$ $\displaystyle 187.5 \pi m^3$

$157.5 \pi m^3$ $\displaystyle 157.5 \pi m^3$

$200 \pi m^3$ $\displaystyle 200 \pi m^3$

$150.5 \pi m^3$ $\displaystyle 150.5 \pi m^3$

Correct answer:

$187.5 \pi m^3$ $\displaystyle 187.5 \pi m^3$

Explanation:

The formula for the volume of a half-cylinder is:

$V = \frac{1}{2} (\pi r^2 h)$ $\displaystyle V = \frac{1}{2} (\pi r^2 h)$

where $\displaystyle r$ is the radius of the base and $\displaystyle h$ is the length of the height.

Plugging in our values, we get:

$V = \frac{1}{2} \pi (5m)^2 (15m)$ $\displaystyle V = \frac{1}{2} \pi (5m)^2 (15m)$

$V = 187.5 \pi m^3$ $\displaystyle V = 187.5 \pi m^3$

Report an Error

Example Question #6 : Other Polyhedrons

Find the volume of the following polyhedron.

Ice_cream_cone

Possible Answers:

$81 \pi m^3+54\sqrt{3} \pi m^3$ $\displaystyle 81 \pi m^3+54\sqrt{3} \pi m^3$

$54 \pi m^3+81\sqrt{3} \pi m^3$ $\displaystyle 54 \pi m^3+81\sqrt{3} \pi m^3$

$81 \pi m^3+81\sqrt{3} \pi m^3$ $\displaystyle 81 \pi m^3+81\sqrt{3} \pi m^3$

$81 \pi m^3+50\sqrt{3} \pi m^3$ $\displaystyle 81 \pi m^3+50\sqrt{3} \pi m^3$

$54 \pi m^3+54\sqrt{3} \pi m^3$ $\displaystyle 54 \pi m^3+54\sqrt{3} \pi m^3$

Correct answer:

$81 \pi m^3+54\sqrt{3} \pi m^3$ $\displaystyle 81 \pi m^3+54\sqrt{3} \pi m^3$

Explanation:

The formula for the volume of the polyhedron is:

$V = V_{cone}+\frac{1}{2}V_{sphere}$ $\displaystyle V = V_{cone}+\frac{1}{2}V_{sphere}$

$V = \frac{\pi r^2 h}{3} +\frac{1}{2} \frac{4\pi r^3}{3}$ $\displaystyle V = \frac{\pi r^2 h}{3} +\frac{1}{2} \frac{4\pi r^3}{3}$

$V = \frac{\pi r^2 h}{3} +\frac{2\pi r^3}{3}$ $\displaystyle V = \frac{\pi r^2 h}{3} +\frac{2\pi r^3}{3}$

Where $\displaystyle r$ is the radius of the cone, $\displaystyle h$ is the height of the cone, and $\displaystyle r$ is the radius of the sphere.

Use the formula for a $\displaystyle 30-60-90$ triangle to find the length of the radius:

$a-a\sqrt{2}-2a$ $\displaystyle a-a\sqrt{2}-2a$

$3\sqrt{3}m-9m-6\sqrt{3}m$ $\displaystyle 3\sqrt{3}m-9m-6\sqrt{3}m$

Plugging in our values, we get:

$V = \frac{\pi (3\sqrt{3}m)^29m}{3}+\frac{2 \pi (3\sqrt{3}m)^3}{3}$ $\displaystyle V = \frac{\pi (3\sqrt{3}m)^29m}{3}+\frac{2 \pi (3\sqrt{3}m)^3}{3}$

$V = \frac{\pi (27m^2)9m}{3}+\frac{2 \pi (81\sqrt{3}m^3)}{3}$ $\displaystyle V = \frac{\pi (27m^2)9m}{3}+\frac{2 \pi (81\sqrt{3}m^3)}{3}$

$V = 81 \pi m^3+54\sqrt{3} \pi m^3$ $\displaystyle V = 81 \pi m^3+54\sqrt{3} \pi m^3$

Report an Error

Example Question #22 : Solid Geometry

Find the volume of the following polyhedron.

Dome

Possible Answers:

$18 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle 18 \pi \sqrt{3}m^3 + 81 \pi m^3$

$24 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle 24 \pi \sqrt{3}m^3 + 81 \pi m^3$

$6 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle 6 \pi \sqrt{3}m^3 + 81 \pi m^3$

$9 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle 9 \pi \sqrt{3}m^3 + 81 \pi m^3$

$27 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle 27 \pi \sqrt{3}m^3 + 81 \pi m^3$

Correct answer:

$9 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle 9 \pi \sqrt{3}m^3 + 81 \pi m^3$

Explanation:

The formula for the volume of the polyhedron is:

$\displaystyle V = (cone)+(cylinder)$

$V = \frac{\pi r^2 h}{3}+\pi r^2 h$ $\displaystyle V = \frac{\pi r^2 h}{3}+\pi r^2 h$

where $\displaystyle r$ is the radius of the cone, $\displaystyle h$ is the height of the cone, $\displaystyle r$ is the radius of the cylinder, and $\displaystyle h$ is the height of the cylinder.

Use the formula for a $\displaystyle 30-60-90$ triangle to find the length of the radius and height of the cone:

$a-a\sqrt{3}-2a$ $\displaystyle a-a\sqrt{3}-2a$

$3m-3\sqrt{3}m-6m$ $\displaystyle 3m-3\sqrt{3}m-6m$

Plugging in our values, we get:

$V = \frac{\pi (3m)^2 (3\sqrt{3}m)}{3}+\pi (3m)^2 (9m)$ $\displaystyle V = \frac{\pi (3m)^2 (3\sqrt{3}m)}{3}+\pi (3m)^2 (9m)$

$V = 9 \pi \sqrt{3}m^3 + 81 \pi m^3$ $\displaystyle V = 9 \pi \sqrt{3}m^3 + 81 \pi m^3$

Report an Error

Example Question #8 : Other Polyhedrons

Find the volume of the following polyhedron.

Ice_cream_cone

Possible Answers:

$128 \sqrt{2} \pi m^3$ $\displaystyle 128 \sqrt{2} \pi m^3$

$108 \sqrt{2} \pi m^3$ $\displaystyle 108 \sqrt{2} \pi m^3$

$118 \sqrt{2} \pi m^3$ $\displaystyle 118 \sqrt{2} \pi m^3$

$138 \sqrt{2} \pi m^3$ $\displaystyle 138 \sqrt{2} \pi m^3$

$148 \sqrt{2} \pi m^3$ $\displaystyle 148 \sqrt{2} \pi m^3$

Correct answer:

$128 \sqrt{2} \pi m^3$ $\displaystyle 128 \sqrt{2} \pi m^3$

Explanation:

The formula for the volume of the polyhedron is:

$V = (cone) + \frac{1}{2}(sphere)$ $\displaystyle V = (cone) + \frac{1}{2}(sphere)$

$V = \frac{1}{3}(\pi r^2)(h)+\frac{1}{2}\left(\frac{4\pi r^3}{3}\right)$ $\displaystyle V = \frac{1}{3}(\pi r^2)(h)+\frac{1}{2}\left(\frac{4\pi r^3}{3}\right)$

where $\displaystyle r$ is the radius of the polyhedron and $\displaystyle h$ is the height of the cone.

Use the formula for a $\displaystyle 45-45-90$ triangle to find the length of the radius and height:

$a-a-a\sqrt{2}$ $\displaystyle a-a-a\sqrt{2}$

$4\sqrt{2}m-4\sqrt{2}m-8m$ $\displaystyle 4\sqrt{2}m-4\sqrt{2}m-8m$

Plugging in our values, we get:

$V = \frac{1}{3}(\pi (4\sqrt{2}m)^2)(4\sqrt{2}m)+\frac{1}{2}\left(\frac{4\pi (4\sqrt{2}m)^3}{3}\right)$ $\displaystyle V = \frac{1}{3}(\pi (4\sqrt{2}m)^2)(4\sqrt{2}m)+\frac{1}{2}\left(\frac{4\pi (4\sqrt{2}m)^3}{3}\right)$

$V = 128 \sqrt{2} \pi m^3$ $\displaystyle V = 128 \sqrt{2} \pi m^3$

Report an Error

Example Question #643 : Geometry

Our backyard pool holds 10,000 gallons. Its average depth is 4 feet deep and it is 10 feet long. If there are 7.48 gallons in a cubic foot, how wide is the pool?

Possible Answers:

133 ft

33 ft

7.48 ft

100 ft

30 ft

Correct answer:

33 ft

Explanation:

There are 7.48 gallons in cubic foot. Set up a ratio:

1 ft³ / 7.48 gallons = x cubic feet / 10,000 gallons

Pool Volume = 10,000 gallons = 10,000 gallons * (1 ft³/ 7.48 gallons) = 1336.9 ft³

Pool Volume = 4ft x 10 ft x WIDTH = 1336.9 cubic feet

Solve for WIDTH:

4 ft x 10 ft x WIDTH = 1336.9 cubic feet

WIDTH = 1336.9 / (4 x 10) = 33.4 ft

Report an Error

Example Question #11 : Solid Geometry

A cube has a volume of 64cm³. What is the area of one side of the cube?

Possible Answers:

16cm

16cm³

16cm²

4cm

4cm²

Correct answer:

16cm²

Explanation:

The cube has a volume of 64cm³, making the length of one edge 4cm (4 * 4 * 4 = 64).

So the area of one side is 4 * 4 = 16cm²

Report an Error

Example Question #2 : How To Find The Length Of An Edge Of A Cube

Given that the suface area of a cube is 72, find the length of one of its sides.

Possible Answers:

$\displaystyle 6$

$2\sqrt{3}$ $\displaystyle 2\sqrt{3}$

$\displaystyle 3$

$3\sqrt{2}$ $\displaystyle 3\sqrt{2}$

$\sqrt{6}$ $\displaystyle \sqrt{6}$

Correct answer:

$2\sqrt{3}$ $\displaystyle 2\sqrt{3}$

Explanation:

The standard equation for surface area is

SA=6a^2 $\displaystyle SA=6a^2$

where $\displaystyle a$ denotes side length. Rearrange the equation in terms of $\displaystyle a$ to find the length of a side with the given surface area:

$a=\sqrt{\frac{SA}{6}}=\sqrt{\frac{72}{6}}=\sqrt{12}=2\sqrt{3}$ $\displaystyle a=\sqrt{\frac{SA}{6}}=\sqrt{\frac{72}{6}}=\sqrt{12}=2\sqrt{3}$

Report an Error

View Tutors

Darian
Certified Tutor

University of Florida, Bachelor in Arts, Public Relations.

View Tutors

Adil
Certified Tutor

Pace University-New York, Master of Arts, Accounting and Business Management. University of the Cumberlands, Master of Scienc...

View Tutors

Alexa
Certified Tutor

Michigan State University, Bachelor of Science, Nutrition Sciences.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Philadelphia, Statistics Tutors in Philadelphia, Statistics Tutors in Dallas Fort Worth, SAT Tutors in Washington DC, GRE Tutors in San Francisco-Bay Area, GRE Tutors in Seattle, Statistics Tutors in San Francisco-Bay Area, Spanish Tutors in San Francisco-Bay Area, MCAT Tutors in Dallas Fort Worth, Chemistry Tutors in Houston

Popular Courses & Classes

ISEE Courses & Classes in Los Angeles, SAT Courses & Classes in Los Angeles, GRE Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Seattle, GRE Courses & Classes in Philadelphia, ACT Courses & Classes in Seattle, GMAT Courses & Classes in Philadelphia, LSAT Courses & Classes in New York City, Spanish Courses & Classes in Atlanta, GMAT Courses & Classes in Phoenix

Popular Test Prep

SSAT Test Prep in Washington DC, MCAT Test Prep in Dallas Fort Worth, ACT Test Prep in Houston, LSAT Test Prep in Los Angeles, SSAT Test Prep in Philadelphia, ACT Test Prep in Miami, LSAT Test Prep in New York City, GRE Test Prep in Denver, GRE Test Prep in Miami, SAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Solid Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Surface Area Of A Polyhedron

Example Question #3 : Other Polyhedrons

Example Question #2 : How To Find The Surface Area Of A Polyhedron

Example Question #21 : Solid Geometry

Example Question #6 : Other Polyhedrons

Example Question #22 : Solid Geometry

Example Question #8 : Other Polyhedrons

Example Question #643 : Geometry

Example Question #11 : Solid Geometry

Example Question #2 : How To Find The Length Of An Edge Of A Cube

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: