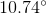We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Plane Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 … 53 54 Next →

Example Question #1 : How To Find The Angle Of A Sector

The length of an arc, , of a circle is $8\pi$ and the radius, , of the circle is . What is the measure in degrees of the central angle, $\theta$ , formed by the arc ?

Possible Answers:

30^o

120^o

60^o

45^o

90^o

Correct answer:

90^o

Explanation:

The circumference of the circle is $2\pi r$ .

$2\pi(16)=32\pi$

The length of the arc S is $8\pi$ .

A ratio can be established:

$\frac{S}{\text{circumference}}=\frac{\theta}{360^o}$

$\frac{8\pi}{32\pi}=\frac{\theta}{360^o}$

Solving for $\theta$ yields 90^o.

Note: This makes sense. Since the arc S was one-fourth the circumference of the circle, the central angle formed by arc S should be one-fourth the total degrees of a circle.

Report an Error

Example Question #1 : How To Find The Angle Of A Sector

Circle

In the circle above, the length of arc BC is 100 degrees, and the segment AC is a diameter. What is the measure of angle ADB in degrees?

Possible Answers:

100

cannot be determined

Correct answer:

Explanation:

Since we know that segment AC is a diameter, this means that the length of the arc ABC must be 180 degrees. This means that the length of the arc AB must be 80 degrees.

Since angle ADB is an inscribed angle, its measure is equal to half of the measure of the angle of the arc that it intercepts. This means that the measure of the angle is half of 80 degrees, or 40 degrees.

Report an Error

Example Question #2 : How To Find The Angle Of A Sector

What is the angle of a sector of area in^2 on a circle having a radius of $15\:in$ ?

Possible Answers:

$15.22^{\circ}$

$0.06^{\circ}$

$22.92^{\circ}$

$3.00^{\circ}$

$72.00^{\circ}$

Correct answer:

$22.92^{\circ}$

Explanation:

To begin, you should compute the complete area of the circle:

$A=\pi r^2$

For your data, this is:

$A=15^2\pi=225\pi$

Now, to find the angle measure of a sector, you find what portion of the circle the sector is. Here, it is:

$\frac{45}{225\pi}$

Now, multiply this by the total 360 degrees in a circle:

$\frac{45}{225\pi}*360=22.918311805212$

Rounded, this is $22.92^{\circ}$ .

Report an Error

Example Question #3 : How To Find The Angle Of A Sector

What is the angle of a sector that has an arc length of 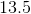13.5 on a circle of diameter ?

Possible Answers:

$35.81^{\circ}$

$14.24^{\circ}$

$10.74^{\circ}$

$194.14^{\circ}$

$128.92^{\circ}$

Correct answer:

$128.92^{\circ}$

Explanation:

The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:

$C=\pi d$

For your data, this means,

$C=12\pi$

Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:

$\frac{13.5}{12\pi}*360=128.9155039044336$

Rounded to the nearest hundredth, this is $128.92^{\circ}$ .

Report an Error

Example Question #1 : How To Find The Area Of A Circle

What is the area of a circle with a radius of ?

Possible Answers:

$64\pi$

$16\pi$

$32\pi$

$8\pi$

Correct answer:

$64\pi$

Explanation:

To find the area of a circle you must plug the radius into in the following equation.

In this case, the radius is , so we plug into .

$A=\pi(8)^2=\pi(64)$

$A=64\pi$

Report an Error

Example Question #2 : How To Find The Area Of A Circle

What is the area of a circle with a radius of 9?

Possible Answers:

$18\pi$

$24\pi$

$81\pi$

$9\pi$

Correct answer:

$81\pi$

Explanation:

To find the area of a circle you must plug the radius into in the following equation

In this case the radius is 9 so we plug it into to get $9^{2}=81$

We then multiply it by $\pi$ to get our answer $A=81\pi$

Report an Error

Example Question #3 : How To Find The Area Of A Circle

Circle_with_radius

Find the area of a circle with a radius of r=6m .

Possible Answers:

$\dpi{100} 63\pi m^{2}$

$36m^{2}$

Not enough information to solve

$36\pi m^{2}$

$\dpi{100} 6\pi m^{2}$

Correct answer:

$36\pi m^{2}$

Explanation:

In order to find the circle's area, utilize the formula $\dpi{100} A=\pi r^{2}$ .

$\dpi{100} A=\pi r^{2}$

$\dpi{100} A=\pi (6m)^{2}$

$\dpi{100} \rightarrow 36\pi m^{2}$

Report an Error

Example Question #4 : How To Find The Area Of A Circle

Circle_with_radius

A circle has a radius r=5in , what is its area?

Possible Answers:

$25\pi in^{2}$

$\dpi{100} 25 in^{2}$

$\dpi{100} 5\pi in^{2}$

Not enough information to solve

$\dpi{100} 25\pi^{2} in^{2}$

Correct answer:

$25\pi in^{2}$

Explanation:

In order to find the circle's area, utilize the formula $\dpi{100} A=\pi r^{2}$ .

$\dpi{100} A=\pi r^{2}$

$A=\pi (5in)^{2}$

$\rightarrow 25\pi in^{2}$

Report an Error

Example Question #5 : How To Find The Area Of A Circle

Circle_with_diameter

A circle has a diameter $D=\pi$ , what is its area?

Possible Answers:

Not enough information to solve

$\pi^{3}$

$\dpi{100} \frac{\pi^{2}}{2}$

$\dpi{100} \frac{\pi^{2}}{4}$

$\frac{\pi^{3}}{4}$

Correct answer:

$\frac{\pi^{3}}{4}$

Explanation:

In order to find the circle's area, utilize the formula $\dpi{100} A=\pi r^{2}$ .

$\dpi{100} A=\pi r^{2}$

However, we need to convert our diameter into a radius.

D=2r

$\pi=2r$

Solve for .

$r=\frac{\pi}{2}$

Insert the radius into the area formula and solve.

$A=\pi (\frac{\pi}{2})^{2}$

$A=\pi*\frac{\pi^{2}}{4}$

$A=\frac{\pi}{1}*\frac{\pi^{2}}{4}$

$\rightarrow \frac{\pi^{3}}{4}$

Report an Error

Example Question #31 : Circles

Circles

Refer to the above drawing. This shows a ring-shaped garden with inner radius 20 feet and outer radius 40 feet. To the nearest square foot, what is the area of the garden?

Possible Answers:

$2,827 \; \textrm{ft}^{2}$

$1,257 \; \textrm{ft}^{2}$

$3,770 \; \textrm{ft}^{2}$

$1,885 \; \textrm{ft}^{2}$

$2,514 \; \textrm{ft}^{2}$

Correct answer:

$3,770 \; \textrm{ft}^{2}$

Explanation:

The total area of the garden is the area of the outer circle - R = 40 - minus that of the inner circle - r=20 .

$A = \pi R^{2} - \pi r^{2} = \pi \cdot 40^{2} - \pi \cdot 20^{2} \approx 5,027 - 1,257 =3,770$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 … 53 54 Next →

View Tutors

Sekou
Certified Tutor

University of New Haven, Bachelor in Arts, Mathematics.

View Tutors

Nicole
Certified Tutor

University of Wisconsin-Madison, Bachelor in Arts, Spanish.

View Tutors

Rodney
Certified Tutor

University of Washington, Master's/Graduate, Economics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Washington DC, Physics Tutors in Washington DC, ACT Tutors in San Francisco-Bay Area, GRE Tutors in Houston, SAT Tutors in Boston, ACT Tutors in Denver, Math Tutors in Philadelphia, Calculus Tutors in Los Angeles, English Tutors in Boston, SSAT Tutors in Phoenix

Popular Courses & Classes

GMAT Courses & Classes in Chicago, SAT Courses & Classes in Phoenix, LSAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Miami, MCAT Courses & Classes in Denver, SSAT Courses & Classes in Chicago, MCAT Courses & Classes in Philadelphia, SAT Courses & Classes in Denver, SSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Houston

Popular Test Prep

ACT Test Prep in Philadelphia, GMAT Test Prep in Chicago, ISEE Test Prep in New York City, ACT Test Prep in Boston, GMAT Test Prep in Washington DC, ISEE Test Prep in Miami, GRE Test Prep in Philadelphia, LSAT Test Prep in Dallas Fort Worth, GRE Test Prep in Miami, SSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Plane Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : How To Find The Angle Of A Sector

Example Question #1 : How To Find The Angle Of A Sector

Example Question #2 : How To Find The Angle Of A Sector

Example Question #3 : How To Find The Angle Of A Sector

Example Question #1 : How To Find The Area Of A Circle

Example Question #2 : How To Find The Area Of A Circle

Example Question #3 : How To Find The Area Of A Circle

Example Question #4 : How To Find The Area Of A Circle

Example Question #5 : How To Find The Area Of A Circle

Example Question #31 : Circles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: