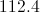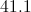We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Applying the Law of Cosines

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Law Of Cosines

In $\Delta ABC$ $\displaystyle \Delta ABC$, AB = 26 $\displaystyle AB = 26$, BC = 32 $\displaystyle BC = 32$, and AC = 23 $\displaystyle AC = 23$. To the nearest tenth, what is $m \angle A$ $\displaystyle m \angle A$ ?

Possible Answers:

$171.3^{ \circ }$ $\displaystyle 171.3^{ \circ }$

$81.3 ^{\circ }$ $\displaystyle 81.3 ^{\circ }$

$98.7^{ \circ }$ $\displaystyle 98.7^{ \circ }$

A triangle with these sidelengths cannot exist.

$81.3 ^{\circ }\textrm{ or } 98.7^{ \circ }$ $\displaystyle 81.3 ^{\circ }\textrm{ or } 98.7^{ \circ }$

Correct answer:

$81.3 ^{\circ }$ $\displaystyle 81.3 ^{\circ }$

Explanation:

By the Triangle Inequality, this triangle can exist, since $\displaystyle 23 + 26 > 32$.

By the Law of Cosines:

$\left ( BC\right )^{2} = \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A$ $\displaystyle \left ( BC\right )^{2} = \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A$

Substitute the sidelengths and solve for $\cos m \angle A$ $\displaystyle \cos m \angle A$ :

$32^{2} = 26^{2} + 23^{2} - 2\cdot 26 \cdot 23 \cdot \cos m \angle A$ $\displaystyle 32^{2} = 26^{2} + 23^{2} - 2\cdot 26 \cdot 23 \cdot \cos m \angle A$

$1,024 =676 + 529 - 1,196 \cdot \cos m \angle A$ $\displaystyle 1,024 =676 + 529 - 1,196 \cdot \cos m \angle A$

$1,024 =1,205 - 1,196 \cdot \cos m \angle A$ $\displaystyle 1,024 =1,205 - 1,196 \cdot \cos m \angle A$

$-181 = - 1,196 \cdot \cos m \angle A$ $\displaystyle -181 = - 1,196 \cdot \cos m \angle A$

$\cos m \angle A = 181 \div 1,196 \approx 0.1513$ $\displaystyle \cos m \angle A = 181 \div 1,196 \approx 0.1513$

$m \angle A \approx \cos^{-1} 0.1513 \approx 81.3 ^{\circ }$ $\displaystyle m \angle A \approx \cos^{-1} 0.1513 \approx 81.3 ^{\circ }$

Report an Error

Example Question #4 : Triangles

A triangle has sides of length 12, 17, and 22. Of the measures of the three interior angles, which is the greatest of the three?

Possible Answers:

$130.1^{\circ }$ $\displaystyle 130.1^{\circ }$

$97.2^{\circ }$ $\displaystyle 97.2^{\circ }$

$119.2^{\circ }$ $\displaystyle 119.2^{\circ }$

$93.6^{\circ }$ $\displaystyle 93.6^{\circ }$

$86.4^{\circ }$ $\displaystyle 86.4^{\circ }$

Correct answer:

$97.2^{\circ }$ $\displaystyle 97.2^{\circ }$

Explanation:

We can apply the Law of Cosines to find the measure of this angle, which we will call :

$c^{2} = a^{2} + b^{2} -2ab \cos C$ $\displaystyle c^{2} = a^{2} + b^{2} -2ab \cos C$

The widest angle will be opposite the side of length 22, so we will set:

c=22 $\displaystyle c=22$, a=12 $\displaystyle a=12$, b=17 $\displaystyle b=17$

$22^{2} = 12^{2} + 17^{2} -2\cdot 12\cdot 17 \cos C$ $\displaystyle 22^{2} = 12^{2} + 17^{2} -2\cdot 12\cdot 17 \cos C$

$484 = 144 + 289 -408 \cos C$ $\displaystyle 484 = 144 + 289 -408 \cos C$

$51= -408 \cos C$ $\displaystyle 51= -408 \cos C$

$\cos C = -\frac{51}{408} = -0.125$ $\displaystyle \cos C = -\frac{51}{408} = -0.125$

$C = \cos^{-1} 0.125 = 97.2^{\circ }$ $\displaystyle C = \cos^{-1} 0.125 = 97.2^{\circ }$

Report an Error

Example Question #2 : Triangles

In $\Delta ABC$ $\displaystyle \Delta ABC$, $m \angle A = 66^{\circ }$ $\displaystyle m \angle A = 66^{\circ }$ , AB = 26 $\displaystyle AB = 26$, and AC = 23 $\displaystyle AC = 23$. To the nearest tenth, what is $\displaystyle BC$?

Possible Answers:

A triangle with these characteristics cannot exist.

41.1 $\displaystyle 41.1$

26.8 $\displaystyle 26.8$

47.9 $\displaystyle 47.9$

112.4 $\displaystyle 112.4$

Correct answer:

26.8 $\displaystyle 26.8$

Explanation:

By the Law of Cosines:

or, equivalently,

$BC =\sqrt{ \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A}$ $\displaystyle BC =\sqrt{ \left ( AB\right )^{2} + \left ( AC\right )^{2} - 2 \cdot AB \cdot AC \cdot \cos m \angle A}$

Substitute:

$BC =\sqrt{ 26^{2} +23^{2} - 2 \cdot 26 \cdot 23 \cdot \cos 66 ^{\circ }}$ $\displaystyle BC =\sqrt{ 26^{2} +23^{2} - 2 \cdot 26 \cdot 23 \cdot \cos 66 ^{\circ }}$

$\approx \sqrt{ 676 +529 - 1,196 \cdot 0.4067}$ $\displaystyle \approx \sqrt{ 676 +529 - 1,196 \cdot 0.4067}$

$\approx \sqrt{ 718.6} \approx 26.8$ $\displaystyle \approx \sqrt{ 718.6} \approx 26.8$

Report an Error

View Tutors

Stephen
Certified Tutor

University of Kansas, Bachelor of Education, Music Teacher Education. University of Kansas, Bachelor in Arts, Music Theory an...

View Tutors

Benyam
Certified Tutor

Case Western Reserve University, Bachelor's (in progress), Statistics & Economics .

View Tutors

Heather
Certified Tutor

University of West Alabama, Bachelor in Arts, English. The University of Alabama, Master of Science, English.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Seattle, Math Tutors in Atlanta, Physics Tutors in Denver, English Tutors in Miami, MCAT Tutors in Dallas Fort Worth, English Tutors in Atlanta, GRE Tutors in Washington DC, Calculus Tutors in Chicago, ISEE Tutors in Boston, Math Tutors in San Francisco-Bay Area

Popular Courses & Classes

MCAT Courses & Classes in Houston, GRE Courses & Classes in Philadelphia, GMAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Boston, GRE Courses & Classes in Chicago, SSAT Courses & Classes in Atlanta, Spanish Courses & Classes in San Diego, GMAT Courses & Classes in Denver, ACT Courses & Classes in Los Angeles, LSAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

SSAT Test Prep in Phoenix, SAT Test Prep in Chicago, SAT Test Prep in Denver, ISEE Test Prep in Philadelphia, SAT Test Prep in San Francisco-Bay Area, SSAT Test Prep in Houston, GMAT Test Prep in Chicago, ACT Test Prep in Los Angeles, SAT Test Prep in San Diego, SSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Applying the Law of Cosines

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Law Of Cosines

Example Question #4 : Triangles

Example Question #2 : Triangles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: