All High School Math Resources
Example Questions
Example Question #41 : Algebra Ii
Simplify the following complex number expression:
Begin by simplifying the radicals using complex numbers:

Multiply the factors:
Simplify. Remember that 

Example Question #12 : Using Expressions With Complex Numbers
Simplify the following complex number expression:
Begin by completing the square:

Multiply the factors:

Simplify. Remember that 

Example Question #13 : Using Expressions With Complex Numbers
Simplify the following complex number expression:
Begin by completing the square:

Now, multiply the factors:

Simplify. Remember that 

Example Question #14 : Using Expressions With Complex Numbers
Simplify the following complex number expression:
Use the FOIL (First, Outer, Inner, Last) to multiply the complex numbers:
Combine like terms and simplify. Remember that 

Example Question #15 : Using Expressions With Complex Numbers
Simplify the following complex number expression:
Begin by multiplying the numerator and denominator by the conjugate of the denominator:

Combine like terms:
Simplify. Remember that 

Example Question #31 : Mathematical Relationships And Basic Graphs
Simplify the following complex number expression:
Begin by multiplying the numerator and denominator by the conjugate of the denominator:
Combine like terms:
Simplify. Remember that 

Example Question #17 : Using Expressions With Complex Numbers
Simplify the following expression:
Simplifying expressions with complex numbers uses exactly the same process as simplifying expressings with one variable. In this case, 
Example Question #11 : Using Expressions With Complex Numbers
Simplify the following complex number expression:
Use the FOIL (First, Outer, Inner, Last) method to expand the expression:
Simplify. Remember that 

Example Question #1 : Radicals
Simplify the expression. Find the positive solution only.
When working in square roots, each component can be treated separately.
Now, we can simplify each term.
Combine the simplified terms to find the answer. Anything outside of the square root is combined, while anything under the root is combined under the root.
Example Question #1 : Radicals
Convert the radical to exponential notation.
Remember that any term outside the radical will be in the denominator of the exponent.
Since 
Certified Tutor
Certified Tutor
All High School Math Resources


















































































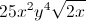



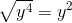

![\small \sqrt[4]{13}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116532/gif.latex)




![\sqrt[b]{x^a}=x^{\frac{a}{b}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88790/gif.latex)
![\sqrt[4]{13}=13^{\frac{1}{4}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88791/gif.latex)



