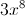All High School Math Resources
Example Questions
Example Question #1 : Simplifying Expressions
Let 



To solve this problem, plug 


Example Question #41 : Basic Single Variable Algebra
Evaluate 
When multiplying an even number of negatives, you get a positive.
When multiplying an odd number of negative, you get a negative.
Example Question #42 : Basic Single Variable Algebra
Evaluate 

When multiplying an odd number of negatives, the answer is negative.
When multiplying an even number of negatives, the answer is positive.
Example Question #41 : Basic Single Variable Algebra
Simplify:
Example Question #41 : Basic Single Variable Algebra
Simplify:


(Like terms are terms that have the same variables with the same exponents. Only like terms can be combined together.)
Example Question #1526 : High School Math
Simplify 
Change the mixed numbers into improper fractions by multiplying the whole number by the denominator and adding the numerator:

Dividing by a fraction is the same as multiplying by the reciprocal, so the problem becomes 
Example Question #1527 : High School Math
Which of the following describes the values of x belonging to the domain of the function 
The domain of a function consists of all of the values of x for which f(x) is defined. When determining the domain of a funciton, the three most important things we want to consider are square roots, logarithms, and denominators of fractions. These tend to signal places where the function is not defined.
First, let's look at the 

Second, we need to look at the natural logarithm. The natural logarithm can only be applied to positive numbers (which don't include zero). Thus, everything within the paranethesis of the natural logarithm must be greater than zero.
There are several ways to solve this inequality. One way is to factor the left side and examine the factors. We know that 

This statement will only be true in two situations; either both factors must be positive, or both must be negative.
We can see that if 




Let's consider the interval 




Third, consider the interval 

To summarize, 

We can see now that f(x) is only defined if 

There is one more piece of information we need to consider--the denominator of f(x). Remember that a fraction is not defined if its denominator equals zero. Thus, if the denominator is equal to zero at a certain value of x, we can't include this value of x in the domain of f(x).
We can set the denominator equal to zero and solve to see if there are any values of x where the denominator would be zero.
Rewrite this as an exponential equation. In general, the equation 

If we put 
We can solve this for x.
So, let's put all of this information together. We know that f(x) is only defined if ALL of these conditions are met:
The only interval for which this is true is if x is greater than (and not equal to) zero but less than (and not equal to) 1. Thus, the domain of f(x) is 
The answer is 
Example Question #42 : Basic Single Variable Algebra
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 

Example Question #2 : Solving Inequalities
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 


So when we solve inequalities with binomials, we must create two scenarios: one where the value inside of the parentheses is positive and one where it is negative. For the negative scenario, we must flip the sign as we normally do for inequalities.
Now we must create our two scenarios:

Notice that in the negative scenario, we flipped the sign of the inequality.


Example Question #3 : Solving Inequalities
Solve for 
Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that 


So when we solve inequalities with binomials, we must create two scenarios: one where the value inside of the parentheses is positive and one where it is negative. For the negative scenario, we must flip the sign as we normally do for inequalities.
Now we must create our two scenarios:

Notice that in the negative scenario, we flipped the sign of the inequality.


All High School Math Resources





















![[x^{1/2}]^{7/3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/181666/gif.latex)





![[x^{m}]^{n}=x^{m\times n}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/27168/gif.latex)