All GRE Subject Test: Math Resources
Example Questions
Example Question #11 : Calculus
What is the range of the function?
Step 1: Find the minimum and maximum range for each equation..
Let's start with 
I will plug in 

Minimum range:
Maximum range:
Step 2: Write the solution in interval notation form:


Answer:
![(-\infty, -1] \cup [9,+\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725519/gif.latex)
Example Question #11 : Gre Subject Test: Math
At what point does the line 
Step 1: Rearrange the terms into the form y=mx+b. Move the 
Step 2: Move the 4 to the other side.
Step 3: When the line crosses the y-axis, the x value is zero. We will plug in 
So, the point where this line crosses the y-axis is
Example Question #11 : Functions And Graphs
What kind of function is this: ![f(x)=\sqrt[3] {x-1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/718623/gif.latex)
Cube-Root Function
Square Function
Cube Function
Rational Function
Cube-Root Function
Step 1: Look at the equation.. ![\sqrt[3] {x-1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/718624/gif.latex)
The function is a cube-root function.
Note:
Square function,
Cube function,
Rational function, 

Example Question #12 : Functions
What kind of function is
Hyperbola
Line
Cubic
Parabola
Cubic
Step 1: To classify any function, find the degree of that function. The degree of a function is the highest exponent.
Step 2: Find degree of 
The degree is 3..
Step 3: Find what kind of function has degree of 3:
A cubic function has a degree of 3...
A square function has a degree of 2
A line has a degree of 1
Example Question #14 : Gre Subject Test: Math
What kind of function is
Parabola
Cubic
Line
Circle
Parabola
Step 1: Define some basic graphs and their functions...
Line functions have an equation 
Parabola (Quadratic functions) have an equation 


Cubic functions have an equation 
Step 2: Determine what type of function is given...
The equation given is a parabola...
Example Question #12 : Functions And Graphs
What kind of function is ![\large y=\sqrt[3] {x+6}-4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/825341/gif.latex)
Absolute Value
Cube-Root Function
Cubic Function
Quadratic Function
Reciprocal Function
Cube-Root Function
Quadratic functions have at least an 
Absolute Functions have 
Cube-Root functions have
The function 
Example Question #1 : Find The Distance Between A Point And A Line
Find the minimum distance between the point 
The minimum distance from the point to the line would be found by drawing a segment perpendicular to the line directly to the point. Our first step is to find the equation of the new line that connects the point to the line given in the problem. Because we know this new line is perpendicular to the line we're finding the distance to, we know its slope will be the negative inverse of the line its perpendicular to. So if the line we're finding the distance to is:
Then its slope is -1/3, so the slope of a line perpendicular to it would be 3. Now that we know the slope of the line that will give the shortest distance from the point to the given line, we can plug the coordinates of our point into the formula for a line to get the full equation of the new line:
Now that we know the equation of our perpendicular line, our next step is to find the point where it intersects the line given in the problem:
So if the lines intersect at x=0, we plug that value into either equation to find the y coordinate of the point where the lines intersect, which is the point on the line closest to the point given in the problem and therefore tells us the location of the minimum distance from the point to the line:
So we now know we want to find the distance between the following two points:

Using the following formula for the distance between two points, which we can see is just an application of the Pythagorean Theorem, we can plug in the values of our two points and calculate the shortest distance between the point and line given in the problem:
Which we can then simplify by factoring the radical:
Example Question #1 : Distance & Midpoint Formulas
What is the shortest distance between the line 
The shortest distance from a point to a line is always going to be along a path perpendicular to that line. To be perpendicular to our line, we need a slope of 
To find the equation of our line, we can simply use point-slope form, using the origin, giving us


Now we want to know where this line intersects with our given line. We simply set them equal to each other, giving us 
If we multiply each side by 

We can then add 

Finally we divide by 

This is the x-coordinate of their intersection. To find the y-coordinate, we plug 


Therefore, our point of intersection must be 
We then use the distance formula 

This give us 
Example Question #2 : Distance & Midpoint Formulas
Find the distance from point 

Draw a line that connects the point and intersects the line at a perpendicular angle.
The vertical distance from the point 

The distance can never be negative.
Example Question #4 : Distance & Midpoint Formulas
Find the distance between point 

Distance cannot be a negative number. The function 
Certified Tutor
Certified Tutor
All GRE Subject Test: Math Resources



![(-\infty,-1]\cup [9,+\infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/725468/gif.latex)










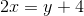











![\large \sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/825344/gif.latex)
![\large \sqrt[3]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/825346/gif.latex)






































