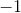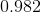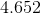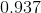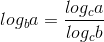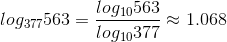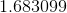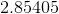We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

GRE Subject Test: Math : Classifying Algebraic Functions

Study concepts, example questions & explanations for GRE Subject Test: Math

Create An Account

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #311 : Gre Subject Test: Math

$Solve\ for\ x: log_{3}(x)=2$

Possible Answers:

$\frac{1}{3}$

Correct answer:

Explanation:

$We\ can\ use\ the\ general\ rule:\ log_{b}(a)=x\\ when\ rewritten\ in\ exponential\ form\ we\ get: b^{x}=a$

$In\ this\ case\ we\ have\ log_{3}(x)=2$

$This\ can\ be\ rewritten\ in\ exponential\ form\ as: 3^2=x$

$We\ know\ that\ 3^2=9;\ so\ x=9$

Report an Error

Example Question #11 : Logarithms

$Rewrite\ as\ one\ log:\ log(a)-(\left log(b)+log(c) \right)$

Possible Answers:

log(a-b-c)

$log\left ( \frac{a}{bc} \right )$

$log\left ( \frac{ab}{c} \right )$

log(a-b+c)

Correct answer:

$log\left ( \frac{a}{bc} \right )$

Explanation:

$When\ condensing\ logs\ we\ must\ remember\ the\ log\ properties:$

$log(x)+log(y)=log(xy): When\ adding;\ we\ multiply.$

$log(x)-log(y)=log\left (\frac{x}{y} \right ): When\ subtracting;\ we\ divide.$

$GIVEN: Rewrite\ as\ one\ log:\ log(a)-(\left log(b)+log(c) \right)\\$

$This\ is\ rewritten\ as:\ log \left (\frac{a}{bc} \right )\\ because\ the\ negative\ will\ be\ distributed\ to\ log(b)\ and\ log(c)$

Report an Error

Example Question #1 : Logarithmic Properties

Rewrite the following expression as a single logarithm

$5log_35x+log_3\frac{1}{4x^3}-log_3x^2$

Possible Answers:

6.06

log_33125x

3.076

$log_3\frac{3125x^3}{9}$

$log_3\frac{3125x^3}{4}$

Correct answer:

6.06

Explanation:

Recall a few properties of logarithms:

1.When adding logarithms of like base, we multiply the inside.

2.When subtracting logarithms of like base, we divide the inside.

3. When multiplying a logarithm by a number, we can raise the inside to that power.

So we begin with this:

$5log_35x+log_3\frac{1}{4x^3}-log_3x^2$

I would start with 3 to simplify the first log.

$log_3(5x)^5+log_3\frac{1}{4x^3}-log_3x^2$

$log_33125x^5+log_3\frac{1}{4x^3}-log_3x^2$

Next, use rule 1 on the first two logs.

$log_3\left(3125x^5\cdot\frac{1}{4x^3}\right)-log_3x^2$

$log_3\left(\frac{3125x^2}{4}\right)-log_3x^2$

Then, use rule 2 to combine these two.

$log_3\left(\frac{3125x^2}{4x^2}\right)=log_3\left(\frac{3125}{4}\right)\approx 6.06$

So our answer is 6.06.

Report an Error

Example Question #131 : Classifying Algebraic Functions

Evaluate:

$3^{3x+3}=27^{2x+2}$

Possible Answers:

$\frac{1}{2}$

$-\frac{1}{2}$

$\frac{4}{13}$

$\frac{2}{3}$

Correct answer:

Explanation:

In order to evaluate the unknown variable, it is necessary to change the base. Looking at the right side of the equation, 27 is equivalent to three cubed.

3^3=27

Therefore, converting the right side of the equation to a base of 3 will allow setting both the left and right side of the exponential terms equal to each other.

$3^{3x+3}=27^{2x+2}$

$3^{3x+3}=3^{3(2x+2)}$

Log both sides to drop the exponents by log properties, and divide the log based 3 on both sides to cancel this term.

Solve for x.

$ln\: 3^(^3^x^+^3^)=ln\:3^3^(^2^x^+^2^)$

3x+3=3(2x+2)

3x+3=6x+6

-3=3x

x=-1

Report an Error

Example Question #1 : Change Of Base

Evaluate the following logarithm:

$log_{377}(563)$

Possible Answers:

1.068

0.982

4.652

1.238

0.937

Correct answer:

1.068

Explanation:

The simplest way to evaluate a logarithm that doesn't have base 10 is with change of base formula:

$log_ba=\frac{log_ca}{log_cb}$

So we have

$log_{377}(563)$

$log_{377}563=\frac{log_{10}563}{log_{10}377}\approx1.068$

Report an Error

Example Question #3 : Change Of Base

$Solve\ for\ x: 3^x=23$

Possible Answers:

2.85405

2.73058

1.89205

1.683099

Correct answer:

2.85405

Explanation:

In order to solve a logarithm, we must first rewrite it in log form:

$3^x=23\ written\ in\ log\ form\ is: log_{3}(23)=x$

To solve for x, we must use the Change of Base:

$log_{3}(23)=\frac{log(23)}{log(3)}$

$\frac{log(23)}{log(3)}=2.85405$

This means that:

$3^{2.85405}=23$

Report an Error

Example Question #1 : Solving Exponential Equations

Find one possible value of , given the following equation:

$343=7^{15t-12}$

Possible Answers:

Cannot be determined from the information given.

t=0

t=5

t=-3

t=1

Correct answer:

t=1

Explanation:

We begin with the following:

$343=7^{15t-12}$

This can be rewritten as

$7^3=7^{15t-12}$

Recall that if you have two exponents with equal bases, you can simply set the exponents equal to eachother. Do so to get the following:

3=15t-12

Solve this to get t.

15=15t

t=1

Report an Error

Example Question #132 : Classifying Algebraic Functions

Solve for .

$4^{2x}=16^{2x-6}$

Possible Answers:

x=6

x=-6

x=4

$x=log \ 2$

Correct answer:

x=6

Explanation:

We need to make the bases equal before attempting to solve for . Since 16=4^2 we can rewrite our equation as

$4^{2x}=4^{2^{2x-6}}$

Remember: the exponent rule $(x^n)^m=x^{n\cdot m}$

$4^{2x}=4^{2(2x-6)}$

Now that our bases are equal, we can set the exponents equal to each other and solve for .

2x=2(2x-6)

2x=4x-12

12=2x

x=6

Report an Error

Example Question #3 : Solving Exponential Equations

Solve for .

$7^{2y}-3^{y+2}=0$

Possible Answers:

y=1

$y=\frac{2\ln3}{2 \ln 7-\ln3}$

y=-1

$y=\frac{2\ln3}{2 \ln 7+\ln3}$

Correct answer:

$y=\frac{2\ln3}{2 \ln 7-\ln3}$

Explanation:

The first step is to make sure we don't have a zero on one side which we can easily take care of:

$7^{2y}=3^{y+2}$

Now we can take the logarithm of both sides using natural log:

$\ln 7^{2y}=\ln 3^{y+2}$

Note: we can apply the Power Rule here $\ln (x^y)=y\ln (x)$

$2y \ln 7=(y+2)\ln3$

$2y \ln 7=y\ln3+2\ln3$

$2y \ln 7-y\ln3=2\ln3$

$y(2 \ln 7-\ln3)=2\ln3$

$y=\frac{2\ln3}{2 \ln 7-\ln3}$

Report an Error

Example Question #4 : Solving Exponential Equations

Solve for .

$3e^{(4x-5)}=24$

Possible Answers:

$x=\frac{\ln21+5}{4}$

$x=\frac{\ln8+5}{4}$

$x=\frac{\ln8-5}{4}$

$x=\ln2+5}$

Correct answer:

$x=\frac{\ln8+5}{4}$

Explanation:

Before beginning to solve for , we need to have a coefficient of :

$e^{(4x-5)}=8$

Now we can take the natural log of both sides:

$\ln e^{(4x-5)}=\ln8$

Note: $\ln (e)=1$

$4x-5=\ln8$

$4x=\ln8+5$

$x=\frac{\ln8+5}{4}$

Report an Error

View Tutors

Virginia
Certified Tutor

Florida Institute of Technology, Bachelor of Science, Mathematics. Webster University, Master of Arts, Information Resources ...

View Tutors

Philipp
Certified Tutor

University of Nevada-Las Vegas, Bachelor of Science, Mechanical Engineering.

View Tutors

Evgenii
Certified Tutor

All GRE Subject Test: Math Resources

2 Diagnostic Tests 148 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Miami, Physics Tutors in Dallas Fort Worth, GRE Tutors in Dallas Fort Worth, Biology Tutors in Chicago, Math Tutors in Philadelphia, Spanish Tutors in New York City, Statistics Tutors in Houston, Computer Science Tutors in San Diego, GMAT Tutors in Boston, SSAT Tutors in Washington DC

Popular Courses & Classes

SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Phoenix, GMAT Courses & Classes in Washington DC, MCAT Courses & Classes in Atlanta, GRE Courses & Classes in Atlanta, LSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Denver, LSAT Courses & Classes in San Diego, ISEE Courses & Classes in Houston, ACT Courses & Classes in Los Angeles

Popular Test Prep

LSAT Test Prep in Washington DC, SAT Test Prep in Atlanta, LSAT Test Prep in Denver, GRE Test Prep in Seattle, LSAT Test Prep in Los Angeles, ACT Test Prep in Seattle, ISEE Test Prep in San Francisco-Bay Area, ACT Test Prep in Phoenix, SAT Test Prep in San Diego, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GRE Subject Test: Math : Classifying Algebraic Functions

Study concepts, example questions & explanations for GRE Subject Test: Math

All GRE Subject Test: Math Resources

Example Questions

Example Question #311 : Gre Subject Test: Math

Example Question #11 : Logarithms

Example Question #1 : Logarithmic Properties

Example Question #131 : Classifying Algebraic Functions

Example Question #1 : Change Of Base

Example Question #3 : Change Of Base

Example Question #1 : Solving Exponential Equations

Example Question #132 : Classifying Algebraic Functions

Example Question #3 : Solving Exponential Equations

Example Question #4 : Solving Exponential Equations

All GRE Subject Test: Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: