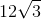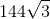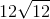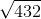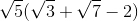GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

Create An Account

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #4 : How To Simplify Square Roots

Which of the following is equivalent to $\frac{x + \sqrt{3}}{3x + \sqrt{2}}$ ?

Possible Answers:

$\frac{3x^{2} - \sqrt{6}}{9x^{2} + 2}$

$\frac{4x + \sqrt{5}}{3x + 2}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

$\frac{3x^{2} + 3x\sqrt{2} + x\sqrt{3} +\sqrt{6}}{9x^{2} - 2}$

$\frac{3x^{2} + \sqrt{6}}{3x - 2}$

Correct answer:

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Explanation:

Multiply by the conjugate and the use the formula for the difference of two squares:

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}$

$\frac{x + \sqrt{3}}{3x + \sqrt{2}}\cdot \frac{3x - \sqrt{2}}{3x - \sqrt{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{(3x)^{2} - (\sqrt{2})^{2}}$

$\frac{3x^{2} -x \sqrt{2} + 3x\sqrt{3} - \sqrt{6}}{9x^{2} - 2}$

Report an Error

Example Question #5 : How To Simplify Square Roots

Which of the following is the most simplified form of:

$\sqrt{468}$

Possible Answers:

$17\sqrt{2}$

$2\sqrt{117}$

$\sqrt{468}$

$6\sqrt{13}$

$4\sqrt{29}$

Correct answer:

$6\sqrt{13}$

Explanation:

First find all of the prime factors of 468

$468=6\ast78=6\ast6\ast13=2\ast3\ast2\ast3\ast13$

So $\sqrt{468}=\sqrt{2\ast2\ast3\ast3\ast13}=2\ast3\sqrt{13}=6\sqrt{13}$

Report an Error

Example Question #11 : How To Simplify Square Roots

What is $\sqrt{432}$ equal to?

Possible Answers:

$6\sqrt{4}$

$12\sqrt{3}$

$144\sqrt{3}$

$6\sqrt{3}$

$12\sqrt{12}$

Correct answer:

$12\sqrt{3}$

Explanation:

$\sqrt{432}$

1. We know that 432=(144)(3) , which we can separate under the square root:

$\sqrt{144\cdot 3}$

2. 144 can be taken out since it is a perfect square: $12\cdot12=144$ . This leaves us with:

$12\sqrt{3}$

This cannot be simplified any further.

Report an Error

Example Question #611 : Gre Quantitative Reasoning

Which of the following is equivalent to:

$\sqrt{210}+\sqrt{55}$ ?

Possible Answers:

$5\sqrt{7}+\sqrt{11}$

$7\sqrt{30}+5\sqrt{11}$

$5\sqrt{462}$

$\sqrt{265}$

$\sqrt{5}(\sqrt{42}+\sqrt{11})$

Correct answer:

$\sqrt{5}(\sqrt{42}+\sqrt{11})$

Explanation:

To begin with, factor out the contents of the radicals. This will make answering much easier:

$\sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}$

They both have a common factor . This means that you could rewrite your equation like this:

$\sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}$

This is the same as:

$\sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}$

These have a common $\sqrt{5}$ . Therefore, factor that out:

$\sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})$

Report an Error

Example Question #1 : Factoring Common Factors Of Squares And Square Roots

Simplify:

$\sqrt{15}-\sqrt{20}+\sqrt{35}$

Possible Answers:

$\sqrt{5}(\sqrt{10}-2)$

$2\sqrt{15}+\sqrt{2}$

$\sqrt{7}-3\sqrt{5}$

$\sqrt{2}(\sqrt{5}+2\sqrt{7})$

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Correct answer:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Explanation:

These three roots all have a in common; therefore, you can rewrite them:

$\sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}$

Now, this could be rewritten:

$\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}$

Now, note that $\sqrt{4}=2$

Therefore, you can simplify again:

$\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}$

Now, that looks messy! Still, if you look carefully, you see that all of your factors have $\sqrt{5}$ ; therefore, factor that out:

$\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})$

This is the same as:

$\sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Report an Error

Example Question #31 : Basic Squaring / Square Roots

Simplify the following:

$\sqrt{125}+\sqrt{245}+\sqrt{80}$

Possible Answers:

$16\sqrt{5}$

$3\sqrt{5}+21\sqrt{2}$

It cannot be simplified any further

$90\sqrt{5}$

$\sqrt{450}$

Correct answer:

$16\sqrt{5}$

Explanation:

Begin by factoring each of the roots to see what can be taken out of each:

$\sqrt{5^3}+\sqrt{7^2*5}+\sqrt{4^2*5}$

These can be rewritten as:

$5\sqrt{5}+7\sqrt{5}+4\sqrt{5}$

Notice that each of these has a common factor of $\sqrt{5}$ . Thus, we know that we can rewrite it as:

$5\sqrt{5}+7\sqrt{5}+4\sqrt{5} = \sqrt{5}(5+7+4) = 16\sqrt{5}$

Report an Error

Example Question #32 : Basic Squaring / Square Roots

Simplify the following:

$\sqrt{40}+\sqrt{20}+\sqrt{160}$

Possible Answers:

$8\sqrt{10}$

$\sqrt{10}(6+\sqrt{2})$

$\sqrt{5}(5 + 2\sqrt{2})$

$4\sqrt{20}$

The expression cannot be simplified any further.

Correct answer:

$\sqrt{10}(6+\sqrt{2})$

Explanation:

Clearly, all three of these roots have a common factor inside of their radicals. We can start here with our simplification. Therefore, rewrite the radicals like this:

$\sqrt{4}\sqrt{10}+\sqrt{2}\sqrt{10}+\sqrt{16}\sqrt{10}$

We can simplify this a bit further:

$2\sqrt{10}+\sqrt{2}\sqrt{10}+4\sqrt{10} = 6\sqrt{10} + \sqrt{2}\sqrt{10}$

From this, we can factor out the common $\sqrt{10}$ :

$6\sqrt{10} + \sqrt{2}\sqrt{10} = \sqrt{10}(6+\sqrt{2})$

Report an Error

Example Question #5 : How To Find The Common Factor Of Square Roots

$\frac{\sqrt{243}}{\sqrt{48}}=$

Possible Answers:

$\frac{9}{4}$

$\frac{81}{16}$

$4\sqrt{3}$

$\frac{3}{2}$

$9\sqrt{3}$

Correct answer:

$\frac{9}{4}$

Explanation:

To attempt this problem, attempt to simplify the roots of the numerator and denominator:

$\frac{\sqrt{243}}{\sqrt{48}}=\frac{\sqrt{3*81}}{\sqrt{3*16}}$

Notice how both numerator and denominator have a perfect square:

$\frac{\sqrt{243}}{\sqrt{48}}=\frac{\sqrt{3*81}}{\sqrt{3*16}}=\frac{9\sqrt3}{4\sqrt3}$

The $\sqrt3$ term can be eliminated from the numerator and denominator, leaving

$\frac{9}{4}$

Report an Error

Example Question #32 : Arithmetic

$\frac{\sqrt{343}}{\sqrt{63}}=$

Possible Answers:

$7\sqrt{7}$

$\frac{49}{9}$

$\frac{7}{3}$

$\frac{3}{7}$

$3\sqrt{3}$

Correct answer:

$\frac{7}{3}$

Explanation:

For this problem, begin by simplifying the roots. As it stands, numerator and denominator have a common factor of in the radical:

$\frac{\sqrt{343}}{\sqrt{63}}=\frac{\sqrt{7*49}}{\sqrt{7*9}}$

And as it stands, this is multiplied by a perfect square in the numerator and denominator:

$\frac{\sqrt{343}}{\sqrt{63}}=\frac{\sqrt{7*49}}{\sqrt{7*9}}=\frac{7\sqrt{7}}{3\sqrt{7}}$

The $\sqrt{7}$ term can be eliminated from the top and bottom, leaving

$\frac{7}{3}$

Report an Error

Example Question #612 : Gre Quantitative Reasoning

$\frac{\sqrt{150}}{\sqrt{48}}=$

Possible Answers:

$\frac{5\sqrt{3}}{4}$

$\frac{5\sqrt{2}}{3}$

$5\sqrt{2}$

$\frac{5\sqrt{2}}{4}$

$\frac{25\sqrt{2}}{16}$

Correct answer:

$\frac{5\sqrt{2}}{4}$

Explanation:

To solve this problem, try simplifying the roots by factoring terms; it may be noticeable from observation that both numerator and denominator have a factor of in the radical:

$\frac{\sqrt{150}}{\sqrt{48}}=\frac{\sqrt{3*50}}{\sqrt{3*16}}$

We can see that the denominator has a perfect square; now try factoring the in the numerator:

$\frac{\sqrt{150}}{\sqrt{48}}=\frac{\sqrt{3*50}}{\sqrt{3*16}}=\frac{\sqrt{3*2*25}}{4\sqrt{3}}$

We can see that there's a perfect square in the numerator:

$\frac{\sqrt{150}}{\sqrt{48}}=\frac{\sqrt{3*50}}{\sqrt{3*16}}=\frac{\sqrt{3*2*25}}{4\sqrt{3}}=\frac{5\sqrt{3*2}}{4\sqrt{3}}$

Since there is a in the radical in both the numerator and denominator, we can eliminate it, leaving

$\frac{5\sqrt{2}}{4}$

Report an Error

All GRE Math Resources

13 Diagnostic Tests 452 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Phoenix, Spanish Tutors in Philadelphia, SAT Tutors in Houston, Reading Tutors in Washington DC, ACT Tutors in Phoenix, Physics Tutors in Denver, ACT Tutors in Atlanta, SSAT Tutors in Philadelphia, Algebra Tutors in San Francisco-Bay Area, Math Tutors in Denver

Popular Courses & Classes

GMAT Courses & Classes in Houston, MCAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Boston, ACT Courses & Classes in Houston, ACT Courses & Classes in Atlanta, SAT Courses & Classes in Houston, GMAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Phoenix, GRE Courses & Classes in Atlanta

Popular Test Prep

LSAT Test Prep in Denver, SAT Test Prep in Phoenix, ACT Test Prep in Atlanta, ACT Test Prep in Houston, GMAT Test Prep in Seattle, LSAT Test Prep in Houston, SSAT Test Prep in New York City, ISEE Test Prep in Phoenix, MCAT Test Prep in Miami, GRE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

Email address:
Your name:
Feedback:

GRE Math : GRE Quantitative Reasoning

Study concepts, example questions & explanations for GRE Math

All GRE Math Resources

Example Questions

Example Question #4 : How To Simplify Square Roots

Example Question #5 : How To Simplify Square Roots

Example Question #11 : How To Simplify Square Roots

Example Question #611 : Gre Quantitative Reasoning

Example Question #1 : Factoring Common Factors Of Squares And Square Roots

Example Question #31 : Basic Squaring / Square Roots

Example Question #32 : Basic Squaring / Square Roots

Example Question #5 : How To Find The Common Factor Of Square Roots

Example Question #32 : Arithmetic

Example Question #612 : Gre Quantitative Reasoning

All GRE Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details