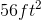All GRE Math Resources
Example Questions
Example Question #11 : Square Roots And Operations
Simplify:
Let's factor the square roots.

Then, multiply the numerator and the denominator by 
Example Question #12 : Square Roots And Operations
Which of the following is equivalent to 
We can definitely eliminate some answer choices. 





Example Question #1 : How To Divide Square Roots
Rationalize the denominator and simplify:
We don't want to have radicals in the denominator. To get rid of radicals, just multiply the numerator and the denominator by that radical.
Remember to distribute the radical in the numerator when multiplying.
This may be the answer; however, the numerator can be simplified. Let's factor out the squares.

Finally, if we factor out a 
Example Question #43 : Arithmetic
Simplify:
Let's get rid of the radicals in the denominator of each individual fraction.

Then find the least common denominator of the fractions, which is 


We can definitely simplify the numerator in the right fraction by factoring out a perfect square of 
Finally, we can factor out a 
That's the final answer.
Example Question #13 : Square Roots And Operations
Simplify:
To get rid of the radical, we need to multiply by the conjugate. The conjugate uses the opposite sign and multiplying by it will let us rationalize the denominator in this problem. The goal is getting an expression of 
This answer is the same as 
Example Question #14 : Square Roots And Operations
Solve for 
To get rid of the radical, multiply top and bottom by 

Square both sides.
Example Question #11 : How To Divide Square Roots
Simplify:



Let's substitute 


Now we can multiply the result by 



We can reduce the resulting 


By multiplying top and bottom by 

The resulting fraction can be simplified:
Example Question #52 : Arithmetic
Simplify.
To get rid of the radical, we need to multiply by the conjugate. The conjugate uses the opposite sign and multiplying by it will let us rationalize the denominator in this problem. The goal is getting an expression of 
Example Question #51 : Arithmetic
Solve for 
You can "break apart" the fractional square root:
into:
Therefore, you can rewrite your equation as:
Now, multiply both sides by 
Now, you can square both sides of your equation and get:
Example Question #1 : How To Multiply Square Roots
The length of a square courtyard is 
What is the area of the courtyard?
The area of a square is length squared. In this case, that would be 


The square root of a base squared is then just the base:

Lastly, we apply the appropriate units, therefore the area of the courtyard is 
All GRE Math Resources