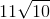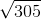All GRE Math Resources
Example Questions
Example Question #581 : Gre Quantitative Reasoning
What is the mode of the following set of numbers?
The mode is the most occuring value in a set. is the mode because it occurs 6 different times in the set.
Example Question #581 : Gre Quantitative Reasoning
Quantitative Comparison
A set of numbers, Set A, has a mean of 4 and a standard deviation of 2. Another set, Set B, has a mean of 100 and a standard deviation of 20.
Quantity A: dispersion of numbers in Set A
Quantity B: dispersion of numbers in Set B
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
Quantity A is greater.
Quantity B is greater.
The standard deviation tells us how much variation, or dispersion, there is on average between the numbers in a set and their mean. Therefore Quantity B is greater, because Set B has a larger standard deviation than Set A.
Example Question #1 : Range
Find the range of the following set of numbers:
Cannot be determined.
The range is the difference between the largest and smallest numbers of a set. The biggest number is 15 and the smallest is 1, so our range is 15 – 1 = 14.
Example Question #583 : Gre Quantitative Reasoning
Quantity A:
The sum of the median and mode of Set G
Quantity B:
The range of Set G
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
Quantity A is greater.
Quantity A is greater.
The median is the middle value in a set of numbers, and the mode is the number that occurs.
In Column A, the median is 6 and the mode is 6, so the sum of the median and the mode of Set G is 12.
The range is the difference between the highest and lowest numbers of the set.
In Column B, the range is 12 – 2 = 10.
Column A is greater than Column B.
Example Question #2 : How To Find Range
Quantity A: The range of Set Q.
Quantity B: The median of Set Q.
The relationship cannot be determined.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The first step of this problem should be to reorder Set Q into numerical order:
The range of a set is the largest value minus the lowest value, so for this set, the range is
The median of a set depends on whether or not there is an even or odd amount of numbers in the set. For a set with values:
Odd:
Even:
Since there is an even number of numbers in this set, the median is
The two quantities are equal.
Example Question #584 : Gre Quantitative Reasoning
Neither x nor y is equal to 0.
xy = 4y/x
Quantity A: x
Quantity B: 2
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
Quantity A is greater.
The relationship cannot be determined from the information given.
Given xy = 4y/x and x and y not 0.
Therefore you are able to divide both sides by 'y' such that:
x = 4/x
Multiply both sides by x:
x2 = 4 or x = +2 or –2.
Because of the fact that x could equal –2, the relationship cannot be determined from the information given.
Example Question #1 : Arithmetic
Quantity A:
Quantity B: 399
The relationship cannot be determined from the information given.
The two quantities are equal.
Quantity A is greater.
Quantitiy B is greater.
The relationship cannot be determined from the information given.
Since is between 10 and 20, it can be any real number between 100 and 400. Therefore, the relationship cannot be determined since could fall anywhere between these two limits, including between 399 and 400.
Example Question #1 : Arithmetic
Quantity A: 9
Quantity B: √(25 + 55)
Quantity A is greater.
Quantity B is greater.
The two quantities are equal.
The relationship cannot be determined from the information given.
Quantity A is greater.
In order to determine the relationship between Quantity A and Quantity B, let's convert both to square roots. In order to do this, we must square Quantity A so it becomes √81 which is equivalent to 9. Now to Quantity B, we must simplify by adding the two values together (25 + 55) to get √80.
√81 is greater than the √80 because 81 is greater than 80. Thus Quantity A is greater.
Example Question #2 : Arithmetic
Simplify:
When simplifying the square root of a number that may not have a whole number root, it's helpful to approach the problem by finding common factors of the number inside the radicand. In this case, the number is 24,300.
What are the factors of 24,300?
24,300 can be factored into:
When there are factors that appear twice, they may be pulled out of the radicand. For instance, 100 is a multiple of 24,300. When 100 is further factored, it is (or 10x10). However, 100 wouldn't be pulled out of the radicand, but the square root of 100 because the square root of 24,300 is being taken. The 100 is part of the24,300. This means that the problem would be rewritten as:
But 243 can also be factored:
Following the same principle as for the 100, the problem would become
because there is only one factor of 3 left in the radicand. If there were another, the radicand would be lost and it would be 9*10*3.
9 and 10 may be multiplied together, yielding the final simplified answer of
Example Question #1 : How To Find The Common Factors Of Squares
To solve the equation , we can first factor the numbers under the square roots.
When a factor appears twice, we can take it out of the square root.
Now the numbers can be added directly because the expressions under the square roots match.
All GRE Math Resources












![G= [2, 4, 5, 5, 6, 6, 6, 10, 12]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/179909/gif.latex)
![SetQ=[2,5,3,7,8,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/520814/gif.latex)
![SetQ=[2,5,3,7,8,7]\rightarrow[2,3,5,7,7,8]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/520815/gif.latex)

![[x_1,x_2,...,x_n]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/520817/gif.latex)








![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267782/gif.latex)
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267778/gif.latex)
![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267774/gif.latex)
![900\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267780/gif.latex)
![9\sqrt[2]{300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267781/gif.latex)
![90\sqrt[2]{270}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267776/gif.latex)
![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267783/gif.latex)
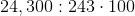

![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267786/gif.latex)


![9\cdot 10\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267789/gif.latex)
![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267790/gif.latex)