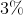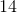All GRE Math Resources
Example Questions
Example Question #31 : How To Find F(X)


The first step is to multiple each side by 

The next step will be to add 

Finally divide both sides by 

Example Question #441 : Algebra
For which value of 
2
6
4
5
3
4
It is important to follow the order of operations for this equation and find a solution that satisfies both F(x) and G(x).
Recall the order of operations is PEMDAS: Parentheses, Exponents, Multiplication/Division, Addition/Subtraction.
The correct answer is 4 because
F(x) = 2x + 3x + (9x/3) = 2(4) + 34 + ((9 * 4)/3) = 101, and
G(x) = (((24 + 44)/2) - 4 * 4) – 5(4) + 1 = 101.
Example Question #353 : Algebra
The function 


24
56
-36
18
36
24
Substitute -1 for 
If you didn’t remember the negative sign, you will have calculated 36. If you remembered the negative sign at the very last step, you will have calculated -36; however, if you did not remember that 
Example Question #443 : Gre Quantitative Reasoning
If the function 



We can take each of the listed transformations of 


Next, take this equation and reflect it across the x-axis. If we reflect a function across the x-axis, then all of its values will be multiplied by negative one. So, 
Lastly, distribute the negative sign to arrive at the final answer.
Example Question #1 : How To Find The Intersection Of A Venn Diagram
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
2
13
25
3
10
3
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
Example Question #441 : Gre Quantitative Reasoning
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
None of the other answers.
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
Example Question #2 : How To Find The Intersection Of A Venn Diagram
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
Example Question #3 : How To Find The Intersection Of A Venn Diagram
At an overpriced department store there are 



A way of solving this problem is by drawing a Venn diagram based on what is known:
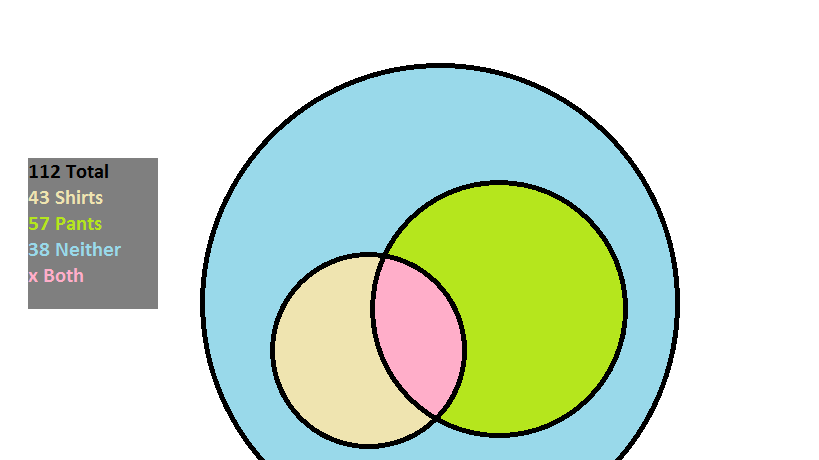
There are 
The amount of individuals that purchased something is given as:
The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since 
The amount that bought both then is:
Example Question #4 : How To Find The Intersection Of A Venn Diagram
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
When you add both class rosters you get a total of 55 students

You must subtract the 7 that are in both because they are counted twice in the 55

The total in neither class will be the total students minus the adjusted enrollment in both classes

Example Question #1 : How To Find The Union Of A Venn Diagram
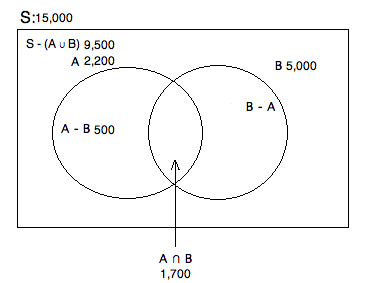
There are 15,000 students at college X. Of those students, 1,700 are taking both ethics and metaphysics this semester. There are 2,200 total students taking ethics. 9,500 students are taking neither of these classes. How many students are taking metaphysics this term?
None of the other answers.
5,000
3300
3800
1600
5,000
The easiest way to understand this problem is to draw a Venn Diagram:
S = Total number of students
A = Total students taking ethics
B = Total students taking metaphysics
A - B = Students taking only ethics
B - A = Students taking only metaphysics
A ∪ B = The total students taking either ethics or metaphysics
A ∩ B = The total students taking both ethics and metaphysics
We know there are 15,000 total and that 9,500 are taking neither class. Therefore, we know that 15,000 - 9,500 = 5,500 are taking at least one of the classes. Based on our prompt, we know that there are 1,700 taking both and that 2,200 are taking ethics. To fiind out how many are taking ONLY ethics, we have to subtract off the amount that are taking ethics and metaphysics. Hence, 2,200 - 1,700 = 500. Finally, if we know that there are 5,500 taking at at least one of these classes, we want to get rid of that portion taking ethics. This will leave us with those who are taking at least metaphysics (regardless of whether or not they are taking ethics): 5,500 - 500 = 5,000.
All GRE Math Resources