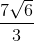All GRE Math Resources
Example Questions
Example Question #2 : Factoring Common Factors Of Squares And Square Roots
Simplify the following:
It cannot be simplified any further
Begin by factoring each of the roots to see what can be taken out of each:
These can be rewritten as:
Notice that each of these has a common factor of 
Example Question #1 : How To Find The Common Factor Of Square Roots
Simplify the following:
The expression cannot be simplified any further.
Clearly, all three of these roots have a common factor 
We can simplify this a bit further:
From this, we can factor out the common 
Example Question #31 : Basic Squaring / Square Roots
To attempt this problem, attempt to simplify the roots of the numerator and denominator:
Notice how both numerator and denominator have a perfect square:
The 
Example Question #613 : Gre Quantitative Reasoning
For this problem, begin by simplifying the roots. As it stands, numerator and denominator have a common factor of 
And as it stands, this 
The 
Example Question #33 : Basic Squaring / Square Roots
To solve this problem, try simplifying the roots by factoring terms; it may be noticeable from observation that both numerator and denominator have a factor of 
We can see that the denominator has a perfect square; now try factoring the 
We can see that there's a perfect square in the numerator:
Since there is a 
Example Question #31 : Arithmetic
Simplify:
None of the other answers
Take each fraction separately first:
(2√3)/(√2) = [(2√3)/(√2)] * [(√2)/(√2)] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6
Similarly:
(4√2)/(√3) = [(4√2)/(√3)] * [(√3)/(√3)] = (4√6)/3 = (4/3)√6
Now, add them together:
√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6
Example Question #32 : Arithmetic
Compare the quantities.
Quantity A:
Quantity B:
The two quantities are equal.
The relationship cannot be determined from the information given.
Quantity A is larger.
Quantity B is larger.
The two quantities are equal.
Begin by breaking down each of the roots in question. Often, for the GRE, your answer arises out of doing such basic "simplification moves".
Quantity A
This is the same as:

Quantity B
This is the same as:

Thus, at the end of working through the proper math, you realize that the two values are equal!
Example Question #2 : Square Roots And Operations
Simplify the following expression:
Begin by factoring out each of the radicals:
For the first two radicals, you can factor out a 

The other root values cannot be simply broken down. Now, combine the factors with 
This is your simplest form.
Example Question #2 : Square Roots And Operations
Solve for 
Note, 
Begin by getting your 
Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:
Now, square both sides:
Solve by dividing both sides by 
Example Question #2 : Square Roots And Operations
Simplify the following expression:
To solve this problem, we must realize that the only way to add or subtract square roots is if the number under to square root is equivalent to each other. Therefore we must find a way to simplify each square root.
First we attempt to simplify the first term,
We break apart the number under the square root and find
Simplifying
Therefore we know that in order to try and simplify the other terms, the number under the square root has to be 3. By removing 
For the second term,
Finally for the last term,
Our new equation becomes
Once all number under the square roots become the same, we can treat it as simple addition/subtraction and solve.
All GRE Math Resources