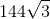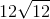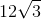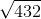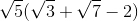All GRE Math Resources
Example Questions
Example Question #3 : How To Simplify Square Roots
Simplify 
Example Question #1 : How To Simplify Square Roots
Simplfy the following radical 
You can rewrite the equation as 
This simplifies to 
Example Question #1 : How To Simplify Square Roots
Which of the following is equal to 
√75 can be broken down to √25 * √3. Which simplifies to 5√3.
Example Question #1 : How To Simplify Square Roots
Simplify 
Rewrite what is under the radical in terms of perfect squares:
Therefore, 
Example Question #3 : How To Simplify Square Roots
What is 
We know that 25 is a factor of 50. The square root of 25 is 5. That leaves 
Example Question #3 : Exponents And Roots
Which of the following is equivalent to 
Multiply by the conjugate and the use the formula for the difference of two squares:




Example Question #1 : How To Simplify Square Roots
Which of the following is the most simplified form of:
First find all of the prime factors of
So
Example Question #1 : Simplifying Square Roots
What is 
1. We know that 
2. 144 can be taken out since it is a perfect square: 
This cannot be simplified any further.
Example Question #2 : Basic Squaring / Square Roots
Which of the following is equivalent to:

To begin with, factor out the contents of the radicals. This will make answering much easier:
They both have a common factor 
This is the same as:
These have a common 
Example Question #3 : Basic Squaring / Square Roots
Simplify:
These three roots all have a 
Now, this could be rewritten:
Now, note that
Therefore, you can simplify again:
Now, that looks messy! Still, if you look carefully, you see that all of your factors have 
This is the same as:
All GRE Math Resources