Assume Statement 1 alone. An exterior angle of a triangle forms a linear pair with the interior angle of the triangle of the same vertex. The two angles, whose measures total , must be two right angles or one acute angle and one obtuse angle. Since , , and  are all obtuse angles, it follows that their respective interior angles - the three angles of  - are all acute. This makes  an acute triangle.

Statement 2 alone provides insufficient information to answer the question. For example, if  and  each measure  and  measures , the sum of the angle measures is ,  and  are congruent, and  is an obtuse angle (measuring more than ); this makes  an obtuse triangle. But  if , , and  each measure , the sum of the angle measures is again ,  and  are again congruent, and all three angles are acute (measuring less than ); this makes  an acute triangle. 

The degree measures of the angles of a triangle add up to a total of 180, so we can set up the following equations:

From the first triangle:

From the second:

These equations form a system of equations that can be solved:

, so

and .

The height of the obtuse isosceles triangle bisects the    angle and forms two congruent right triangles. The hypotenuse of each of these triangles is either side of equivalent length, and we can see that the base of either triangle makes up half of the hypotenuse of the obtuse isosceles triangle. Because we know the angle opposite each base is half of  ,  or  ,  we can use the sine of this angle to find the length of the base. As there are two congruent right triangles that make up the obtuse isosceles triangle, the length of either base makes up half of the overall hypotenuse, so we then multiply the result by    to obtain the final answer. In the following solution,    is the length of the base of one of the right triangles,    is the length of the two equivalent sides, and    is the length of the hypotenuse:

Use Heron's formula:

where , and

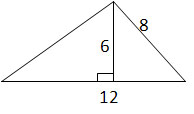
In this problem, the base is 12 and the height is 6. Therefore:

The figure is a composite of a rectangle and a triangle, as shown:

The rectangle has area 

The triangle has area 

The total area of the figure is 

The only restriction on the measure of the vertex angle of an isosceles triangle is the restriction on any angle of a triangle - that it fall between  and , noninclusive. If  is any number in that range, each base angle, the two being congruent, will measure , which will fall in the acceptable range.

Since all of these measures fall in that range, the correct response is that all are allowed.

The easiest way to solve this is to graph the three lines and to observe the dimensions of the resulting triangle. It helps to know the coordinates of the three points of intersection, which we can do as follows:

The intersection of  and the -axis - that is, the line  can be found with some substitution:

The lines intersect at 

The intersection of  and the  -axis can be found the same way:

These lines intersect at 

The intersection of  and   can be found via the substitution method:

The lines intersect at 

The triangle therefore has these three vertices. It is shown below.

As can be seen, it is a triangle with base 9 and height 12, so its area is 

The vertical segment connecting  and  can be seen as the base of this triangle; this base has length . The height is the perpendicular (horizontal) distance from  to this segment, which is 6, the same as the -coordinate of this point. The area of the triangle is therefore 

.

We can view the horizontal segment connecting , and  as the base; its length wiill be . The height will be the perpendicular (vertical) distance to this segment from the opposite point , which is , the -coordinate; therefore, the area of the triangle will be half the product of these two numbers, or

.