All GMAT Math Resources
Example Questions
Example Question #46 : Equilateral Triangles
Which, if either, is greater: the perimeter of equilateral triangle 

Statement 1: The midpoint of 
Statement 2: The midpoint of 
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
For simplicity's sake, we will assume that 
We will also need the circumference formula 
Assume Statement 1 alone. Since the midpoint of 




Assume Statment 2 alone. Since the circle has as a radius the segment from 




Either statement alone establishes that the circumference of the circle is greater than 3, the perimeter of 
Example Question #47 : Equilateral Triangles
Given three equilateral triangles 


Statement 1:
Statement 2:
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
Assume both statements to be true. From Statement 1, since 







Example Question #48 : Equilateral Triangles
Given three equilateral triangles 


Statement 1: A circle with diameter equal to the length of 

Statement 2: A circle with diameter equal to the length of 

BOTH statements TOGETHER are insufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Assume Statement 1 alone, and examine the diagram below, which shows a circle circumscribed about 

The diameter, which is equal to 




If Statement 2 alone is assumed, then, similarly, 


From the two statements together, however, 
Example Question #49 : Equilateral Triangles
Which, if either, of equilateral triangles 

Statement 1:
Statement 2:
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
If we let 



Statement 1:
Statement 2:
Since the perimeter of an equilateral triangle is three times its common sidelength, comparison of the lengths of the sides is all that is necessary to determine which triangle, has the greater perimeter. The question can therefore be reduced to asking which of 

Statement 1 alone is not sufficient to yield an answer:
Case 1:
Case 2:
Both cases satisfy Statement 1, but in the first case, 



Now assume both statements to be true. The two equations together comprise a system of equations:
Multiply the first equation by 3 and the second by 
Now substitute back:

Example Question #50 : Equilateral Triangles
Given an equilateral triangle 


Statement 1:
Statement 2:
BOTH statements TOGETHER are insufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Assume Statement 1 alone. Since in 









and 
Statement 2 alone gives insufficient information, since we know nothing about the second leg or the hypotenuse of 
Case 1: Let 











Case 2: Let 





Example Question #2571 : Gmat Quantitative Reasoning
Find the perimeter of the equilateral triangle.
- A side measures
.
- The area is
.
Each statement alone is sufficient to answer the question.
Statement 2 alone is sufficient, but statement 1 alone is not sufficient to answer the question.
Statement 1 alone is sufficient, but statement 2 alone is not sufficient to answer the question.
Both statements taken together are sufficient to answer the question, but neither statement alone is sufficient.
Statements 1 and 2 are not sufficient, and additional data is needed to answer the question.
Each statement alone is sufficient to answer the question.
Recall the formula for perimeter of a triangle.
where 
Statement 1: We're given the length of the side so all we need to do is plug this value into the equation.
Statement 2: We're given the area so we first need to solve for the side length.
Now we can plug the value into the equation, like we did in Statement 1.
Example Question #1 : Right Triangles
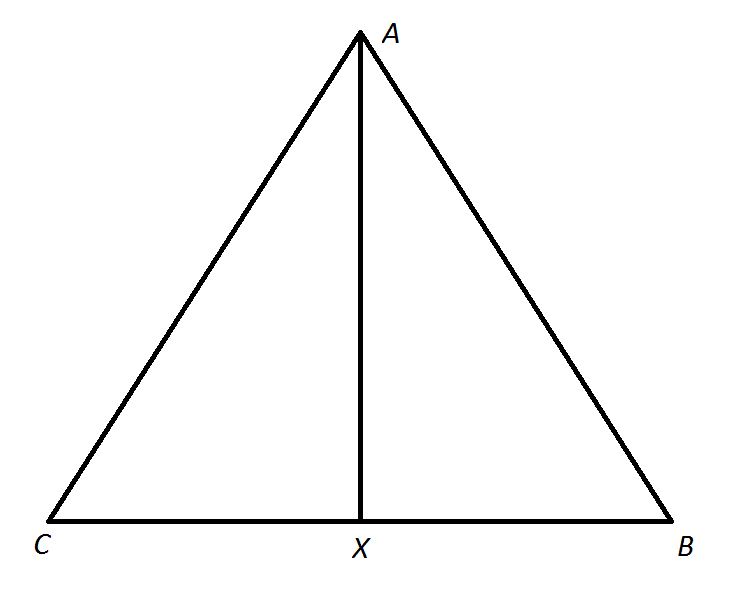
Note: Figure NOT drawn to scale.
Refer to the above diagram.
True or false:
Statement 1: 
Statement 2: 

BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
To prove triangle congruence, we need to establish some conditions involving side and angle congruence.
We know 
If we only assume Statement 1, then we know that 


Example Question #1 : Right Triangles
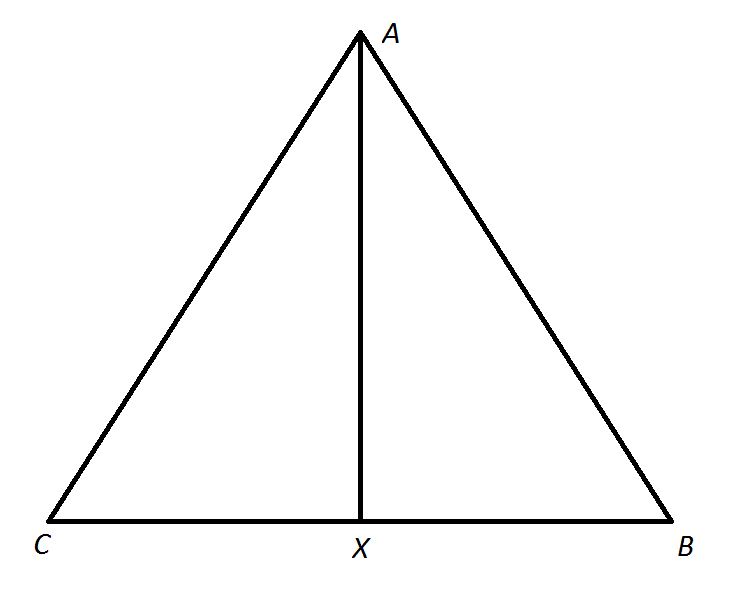
Note: Figure NOT drawn to scale.
Refer to the above diagram.
True or false:
Statement 1: 

Statement 2: 

BOTH statements TOGETHER are insufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
To prove triangle congruence, we need to establish some conditions involving side and angle congruence.
We know 
From Statement 1 alone, by definition, 




From Statement 2 alone,we know that 
Example Question #1 : Right Triangles
Given: 

True or false: 
Statement 1:
Statement 2:
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are insufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
Assume Statement 1 alone. If 



Now assume both statements to be true.
Suppose 

Similarly, if 

and 



Example Question #3 : Right Triangles
Given: 

True or false: 
Statement 1: 
Statement 2:
BOTH statements TOGETHER are insufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
EITHER statement ALONE is sufficient to answer the question.
Statement 1 ALONE is sufficient to answer the question, but Statement 2 ALONE is NOT sufficient to answer the question.
Statement 2 ALONE is sufficient to answer the question, but Statement 1 ALONE is NOT sufficient to answer the question.
BOTH statements TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient to answer the question.
From Statement 1 alone, we are only give one angle congruency and one side congruency, which, without further information, is not enough to prove or to disprove triangle congruence. By a similar argument, Statement 2 alone is not sufficient either.
Assume both statements are true. By Statement 1, the hypotenuses are congruent, and by Statement 2, one pair of corresponding legs are congruent. These are the conditions of the Hypotenuse Leg Theorem, so 
All GMAT Math Resources









































