We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

GED Math : Supplementary Angles

Study concepts, example questions & explanations for GED Math

Create An Account

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 Next →

Example Question #1 : Supplementary Angles

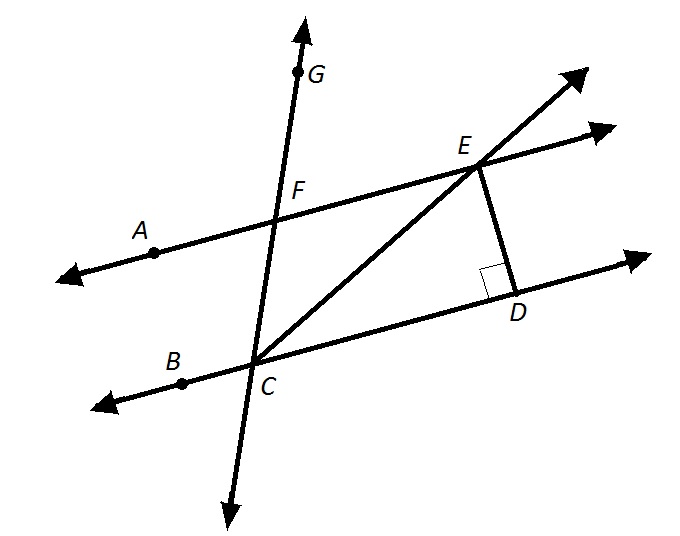
Thingy

Refer to the above diagram.

$\overleftrightarrow{AE} ||\overleftrightarrow{BD}$ ; $m \angle BCE = 136^{\circ }$ . Evaluate $m \angle CED$ .

Possible Answers:

$54 ^{\circ }$

$56 ^{\circ }$

$46 ^{\circ }$

$44 ^{\circ }$

Correct answer:

$46 ^{\circ }$

Explanation:

$\angle BCE$ and $\angle ECD$ form a linear pair, so they are supplementary - that is, their degree measures total $180^{\circ }$ , so

$m \angle BCE + m\angle ECD =180^{\circ }$

$136^{\circ } + m\angle ECD =180^{\circ }$

$m\angle ECD =180^{\circ } - 136 ^{\circ } = 44^{\circ }$

$m \angle CED$ and $\angle ECD$ are acute angles of right triangle $\Delta ECD$ , so they are complementary - that is, their degree measures total $90^{\circ }$ , so

$m \angle CED + m\angle ECD =90^{\circ }$

$m \angle CED + 44 ^{\circ } =90^{\circ }$

$m \angle CED =90^{\circ } - 44 ^{\circ } = 46 ^{\circ }$

Report an Error

Example Question #2 : Supplementary Angles

Angles A, B, and C are supplementary. The measure of angle A is 5x + 15 . The measure of angle B is 2x + 25 . The measure for angle C is 2x + 14 . Find the value of .

Possible Answers:

x = 10

x= 14

x = -2

x = 24

x = 16

Correct answer:

x= 14

Explanation:

Since angles A, B, and C are supplementary, their measures add up to equal 180 degrees. Therefore we can set up the equation as such:

A + B + C =180

-or-

5x + 15 + 2x + 25 + 2x + 15 = 180

Combine like terms and solve for :

9x + 54 = 180

9x = 126

x = 14

Report an Error

Example Question #3 : Supplementary Angles

Angles A and B are supplementary. The measure of angle A is 17x + 20 . The measure of Angle B is -2x + 10 . Find the value of .

Possible Answers:

x = 15

No solution

x = -10

x = 5

x = 10

Correct answer:

x = 10

Explanation:

Since angles A and B are supplementary, thier measurements add up to equal 180 degrees. Therefore we can set up our equation like such:

A + B = 180

-or-

17x + 20 + -2x + 10 = 180

Combine like terms and solve for :

15x + 30 = 180

15x = 150

x = 10

Report an Error

Example Question #4 : Supplementary Angles

Angles A, B, and C are supplementary. The measure of angle A is 10x + 4 . The measure of angle B is 5x - 6 . The measure for angle C = 3x + 2 . What are the measure for the three angles?

Possible Answers:

$Angle A = 114^{\circ}$

$Anbgle B = 32^{\circ}$

$Angle C = 36^{\circ}$

$Angle A = 104^{\circ}$

$Angle B = 44^{\circ}$

$Angle C = 32^{\circ}$

$Angle A = 44^{\circ}$

$Angle B = 32^{\circ}$

$Angle C = 104^{\circ}$

$Angle A = 120^{\circ}$

$Angle B = 40^{\circ}$

$Angle C = 20^{\circ}$

No solution

Correct answer:

$Angle A = 104^{\circ}$

$Angle B = 44^{\circ}$

$Angle C = 32^{\circ}$

Explanation:

Since angles A, B, and C are supplementary, their measures add up to equal 180 degrees. Therefore we can set up an equation as such:

A + B + C = 180

-or-

10x + 4 + 5x - 6 + 3x + 2 = 180

Combine like terms and solve for x:

18x = 180

x = 10

Plug back into the three angle measurements:

Angle A = 10(10) + 4

Angle A = 100 + 4 4

Angle A = 104

Angle B = 5(10) - 6

Angle B = 50 -6

Angle B = 46

Angle C = 3(10) + 2

Angle C = 30 + 2

Angle C = 32

Report an Error

Example Question #1 : Supplementary Angles

If a set of angles are supplementary, what is the other angle if one angle is 101 degrees?

Possible Answers:

Correct answer:

Explanation:

Two angles that are supplementary must add up to 180 degrees.

To find the other angle, subtract 101 from 180.

180-101=79

The answer is:

Report an Error

Example Question #1 : Supplementary Angles

What angle is supplementary to 54 degrees?

Possible Answers:

126

116

136

Correct answer:

126

Explanation:

Supplementary angles must add up to 180 degrees.

To find the other angle, we will need to subtract 54 from 180.

180-54 = 126

The answer is: 126

Report an Error

Example Question #7 : Supplementary Angles

If and are supplementary angles, what must be a possible angle?

Possible Answers:

144

120

160

Correct answer:

144

Explanation:

The sum of the two angles supplement to each other will add up to 180 degrees.

Set up the equation.

2x+8x = 180

Solve for .

10x = 180

Divide by 10 on both sides.

$\frac{10x }{10}= \frac{180}{10}$

x=18

Substitute x=18 for and , and we have 36 and 144, which add up to 180.

The answer is: 144

Report an Error

Example Question #8 : Supplementary Angles

If the angles x+1 and 2x-1 are supplementary, what is the value of ?

Possible Answers:

180

Correct answer:

180

Explanation:

Supplementary angles sum to 180 degrees.

Set up an equation to solve for .

x+1+2x-1 = 180

3x = 180

x=60

Substitute this value to .

3(60) = 180

The answer is: 180

Report an Error

Example Question #9 : Supplementary Angles

Suppose there are two angles. If a given angle is 2x-6 , and both angles are supplementary, what must be the other angle?

Possible Answers:

2x-186

174-2x

186-2x

Correct answer:

186-2x

Explanation:

Supplementary angles add up to 180 degrees.

This means we will need to subtract the known angle quantity from 180.

180-(2x-6)

Distribute the negative.

180-2x+6 = 186-2x

The answer is: 186-2x

Report an Error

Example Question #10 : Supplementary Angles

If an angle given is $\frac{2}{3}\pi$ radians, what is the other angle if both angles are supplementary?

Possible Answers:

$\frac{1}{3}\pi$

$\frac{4}{3}\pi$

$\frac{5}{3}\pi$

$2\pi$

$\frac{2}{3}\pi$

Correct answer:

$\frac{1}{3}\pi$

Explanation:

Note that supplementary angles sum up to 180 degrees or equal to $\pi$ radians.

Subtract the known angle from pi.

$\pi-\frac{2}{3}\pi = \frac{1}{3}\pi$

The answer is: $\frac{1}{3}\pi$

Report an Error

← Previous 1 2 3 4 5 6 Next →

View Tutors

Bethany
Certified Tutor

Union College, Bachelor of Science, Elementary School Teaching. Western Governors University, Master of Science, Curriculum a...

View Tutors

Manqoba
Certified Tutor

Marist College, Bachelor of Science, Business Administration and Management.

View Tutors

Zahid
Certified Tutor

kurukshetra university haryana , Master's/Graduate, Civil engineering.

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in San Diego, French Tutors in San Diego, Physics Tutors in Los Angeles, Math Tutors in Phoenix, Calculus Tutors in Boston, Calculus Tutors in Miami, SAT Tutors in Chicago, Statistics Tutors in Houston, French Tutors in Phoenix, Spanish Tutors in Atlanta

Popular Courses & Classes

SSAT Courses & Classes in Houston, GRE Courses & Classes in Washington DC, LSAT Courses & Classes in Houston, ISEE Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in New York City, MCAT Courses & Classes in Miami, SAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Houston, LSAT Courses & Classes in Atlanta, GRE Courses & Classes in Boston

Popular Test Prep

SSAT Test Prep in Philadelphia, MCAT Test Prep in San Francisco-Bay Area, GMAT Test Prep in Los Angeles, GRE Test Prep in Philadelphia, SSAT Test Prep in Boston, GRE Test Prep in Washington DC, MCAT Test Prep in Miami, GRE Test Prep in Chicago, MCAT Test Prep in Phoenix, LSAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GED Math : Supplementary Angles

Study concepts, example questions & explanations for GED Math

All GED Math Resources

Example Questions

Example Question #1 : Supplementary Angles

Example Question #2 : Supplementary Angles

Example Question #3 : Supplementary Angles

Example Question #4 : Supplementary Angles

Example Question #1 : Supplementary Angles

Example Question #1 : Supplementary Angles

Example Question #7 : Supplementary Angles

Example Question #8 : Supplementary Angles

Example Question #9 : Supplementary Angles

Example Question #10 : Supplementary Angles

All GED Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: