All Common Core: High School - Geometry Resources
Example Questions
Example Question #1 : Explain How The Criteria For Triangle Congruence (Asa, Sas, And Sss) Follow From The Definition Of Congruence In Terms Of Rigid Motions.
What is rigid motion?
Any way of moving a figure such that the relative distance between the points/vertices of the figure stay the same and the relative position of the points/vertices of the figure stay the same
Any way of moving a figure such that the relative distance between the points/vertices of the figure stay the same but the position can differ
Any way of moving a figure such that the relative position of the points/vertices of the figure stay the same but the distance between points/vertices can differ
Any way of moving a figure
Any way of moving a figure such that the relative distance between the points/vertices of the figure stay the same and the relative position of the points/vertices of the figure stay the same
Rigid motion follows these criteria because the motion is rigid meaning that everything that is moving stays the same except for the location of the entire figure. There are three common types of rigid motion; translation, reflection, and rotation.
Example Question #461 : High School: Geometry
In terms of rigid motion, how do we know when two figures are congruent to one another?
Two figures are congruent if there is a sequence of rigid motions that maps at least two vertices to another
Two figures are congruent if there is a sequence of rigid motions that maps one figure to another
Two figures are congruent if they meet the criteria of all three of the following theorems: SAS, ASA, SSS
Two figures are congruent if they meet the criteria of one of the following theorems: SAS, ASA, SSS
Two figures are congruent if there is a sequence of rigid motions that maps one figure to another
This is the correct definition in terms of rigid motions. Some of the other options are correct definitions for congruence but do not mention the criteria of there being rigid motion between the two figures. An example of this is that 



Example Question #462 : High School: Geometry
The following two triangles are congruent by the SAS Theorem. What are the series of rigid motions that map them to one another? (Figures not to scale)
Reflection, rotation
Rotation
Translation
Translation, rotation, reflection
Translation, rotation, reflection
First, we need to establish a vector that maps at least one pair of vertices. We will use 


Now they share a vertex and we are able to rotate them together mapping 



Now we can reflect across 






So the order of the series of rigid motions is translation, rotation, reflection.
Example Question #463 : High School: Geometry
True or False: If two triangles are congruent through SAS Theorem and share a vertex, they will follow the rigid motions of rotation and reflection.
False
True
True
Consider the triangles 






Now we can reflect across 




Now we are left with the two congruent triangles lying on top of one another, proving that the rigid motions that map these two triangles to one another are rotation and reflection.
Example Question #464 : High School: Geometry
Triangles that share a side and follow the SSS criteria for congruence follow which of the following rigid motions?
Rotation
Reflection
None of the answer choices are correct
Translation
Reflection
Consider the following triangles, 










Example Question #465 : High School: Geometry
True or False: The following triangles are congruent by two different methods:

False
True
True
Let’s first begin by showing that these two triangles are congruent through a series of rigid motions. Let’s use our point of reference be 





Now we will show that these two triangles are congruent through another theorem. We see that there are two pairs of corresponding congruent angles, 

Example Question #466 : High School: Geometry
Tell why the following triangles are congruent both by rigid motions and one of the three triangle congruence theorems.

SAS, translation
SSS, reflection
SSS, rotation
SAS, reflection
SSS, reflection
We can see that 





Example Question #111 : Congruence
Through which rigid motion are the following triangles related by?

None of the choices are correct
Rotation
Translation
Reflection
Reflection
This becomes more clear with the orange line between the two triangles. If flipped over this orange line, the two figures would match up their corresponding congruent parts creating the same triangle.

Example Question #468 : High School: Geometry
Give an informal proof that proves the following two triangles are congruent by the SAS Theorem and by a series of rigid motions.

The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 



The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 



The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 



The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 



The SAS Theorem states that if two triangles share two pairs of corresponding congruent sides are congruent and their included angle is also congruent, then these two triangles are congruent. We are given that 



Example Question #471 : High School: Geometry
The following two triangles are congruent by the ASA Theorem. What are the series of rigid motions that map them to one another?
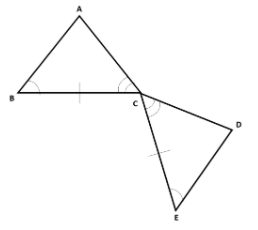
Rotation, reflection
Reflection, translation
Translation
Translation, rotation
Rotation, reflection
First, the two triangles 











Now we can reflect the triangle 








So the order of rigid motions is rotation, reflection.
Certified Tutor
All Common Core: High School - Geometry Resources





