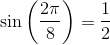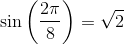This question is testing one's ability to understand the trigonometric relationships and how the relate to the unit circle for solving problems.

For the purpose of Common Core Standards, "Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle." falls within the Cluster A of "Extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF-TF.A.2). 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Plot the line that connects the origin to the point .

Step 2: Use right triangles and the unit circle to identify the trigonometric characteristics of the describe situation. 

The unit circle is an extremely helpful tool in solving trigonometric problems. For the purpose of trigonometry, the unit circle is located at the origin and has a radius of one unit. This is because right triangles can be formed using the x axis as one leg of the triangle and the line from the origin to a point on the circle as the hypotenuse with a measurement of one.

Therefore, the point on the circle has coordinates of  for the angle that is created by the x axis and the hypotenuse. It is important to know that

 and can be found using the triangle that is created on the unit circle.

Recall that using trigonometric identities tangent is,

For this particular question,

Step 3: Answer the question.

This question is testing one's ability to understand the trigonometric relationships and how the relate to the unit circle for solving problems.

For the purpose of Common Core Standards, "Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle." falls within the Cluster A of "Extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF-TF.A.2). 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Plot the line that connects the origin to the point .

Step 2: Use right triangles and the unit circle to identify the trigonometric characteristics of the describe situation. 

The unit circle is an extremely helpful tool in solving trigonometric problems. For the purpose of trigonometry, the unit circle is located at the origin and has a radius of one unit. This is because right triangles can be formed using the x axis as one leg of the triangle and the line from the origin to a point on the circle as the hypotenuse with a measurement of one.

Therefore, the point on the circle has coordinates of  for the angle that is created by the x axis and the hypotenuse. It is important to know that

 and can be found using the triangle that is created on the unit circle.

For this particular question,

Step 3: Answer the question.

This question is testing one's ability to understand the trigonometric relationships and how the relate to the unit circle for solving problems.

For the purpose of Common Core Standards, "Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle." falls within the Cluster A of "Extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF-TF.A.2). 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Plot the line that connects the origin to the point .

Step 2: Use right triangles and the unit circle to identify the trigonometric characteristics of the describe situation. 

The unit circle is an extremely helpful tool in solving trigonometric problems. For the purpose of trigonometry, the unit circle is located at the origin and has a radius of one unit. This is because right triangles can be formed using the x axis as one leg of the triangle and the line from the origin to a point on the circle as the hypotenuse with a measurement of one.

Therefore, the point on the circle has coordinates of  for the angle that is created by the x axis and the hypotenuse. It is important to know that

 and can be found using the triangle that is created on the unit circle.

For this particular question,

Step 3: Answer the question.

This question is testing one's ability to understand the trigonometric relationships and how the relate to the unit circle for solving problems.

For the purpose of Common Core Standards, "Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle." falls within the Cluster A of "Extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF-TF.A.2). 

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Step 1: Plot the line that connects the origin to the point .

Step 2: Use right triangles and the unit circle to identify the trigonometric characteristics of the describe situation. 

The unit circle is an extremely helpful tool in solving trigonometric problems. For the purpose of trigonometry, the unit circle is located at the origin and has a radius of one unit. This is because right triangles can be formed using the x axis as one leg of the triangle and the line from the origin to a point on the circle as the hypotenuse with a measurement of one.

Therefore, the point on the circle has coordinates of  for the angle that is created by the x axis and the hypotenuse. It is important to know that

 and can be found using the triangle that is created on the unit circle.

For this particular question,

Step 3: Answer the question.

This question tests one's ability to understand the connection between special triangles (30-60-90 and 45-45-90), trigonometric functions related to them (sine, cosine, tangent), and the corresponding degree/radian on the unit circle. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each  pair that lies on the circle can be found by creating a right triangle that has a base on the -axis and a hypotenuse that is from the center of the circle to the desired point on the edge of the circle. The height of the triangle is the vertical line that connects the point on the circle's edge to the -axis.

For the purpose of Common Core Standards, understanding "use special triangles to determine geometrically the values of sine, cosine, tangent for " , falls within the Cluster A of "extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF.TF.A).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Possible approaches to solving this problem:

I. Plot the angle on the unit circle to find the .

II. Identify the special triangle that corresponds to the angle.

III. Using memorization of the unit circle.

For this particular question let's us approach II.

Step 1: Simplify the angle if possible.

Step 2: Identify the special right triangle that corresponds to the angle.

Let's convert the angle to degrees to more easily see the special right triangle that it creates.

Therefore the special triangle that is created with  is 30-60-90 degree triangle. The angle which is made at the origin will be 60 degrees and the length of the segment from the origin to the edge of the unit circle is one by definition.

Step 3: Calculate the side lengths of the special triangle.

From here, recall that the special 30-60-90 degree triangle has the following side identities.

Substituting in one for the hypotenuse, the short and long leg of the triangle can be found.

It is important to remember that the short side of the triangle is on the -axis and adjacent to . The long side is the vertical line that is parallel to the -axis and opposite of .

Step 4: Calculate sine, cosine, and tangent.

Recall the following trigonometric identities.

From Step 2, 

Substituting the values found in Step 2 into the above identities is as follows.

This question tests one's ability to understand the connection between special triangles (30-60-90 and 45-45-90), trigonometric functions related to them (sine, cosine, tangent), and the corresponding degree/radian on the unit circle. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each  pair that lies on the circle can be found by creating a right triangle that has a base on the -axis and a hypotenuse that is from the center of the circle to the desired point on the edge of the circle. The height of the triangle is the vertical line that connects the point on the circle's edge to the -axis.

For the purpose of Common Core Standards, understanding "use special triangles to determine geometrically the values of sine, cosine, tangent for " , falls within the Cluster A of "extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF.TF.A).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Possible approaches to solving this problem:

I. Plot the angle on the unit circle to find the .

II. Identify the special triangle that corresponds to the angle.

III. Using memorization of the unit circle.

For this particular question let's us approach II.

Step 1: Simplify the angle if possible.

Step 2: Identify the special right triangle that corresponds to the angle.

Let's convert the angle to degrees to more easily see the special right triangle that it creates.

Therefore the special triangle that is created with  is 45-45-90 degree triangle. The angle which is made at the origin will be 45 degrees and the length of the segment from the origin to the edge of the unit circle is one by definition.

Step 3: Calculate the side lengths of the special triangle.

From here, recall that the special 45-45-90 degree triangle has the following side identities.

Step 4: Calculate sine.

Recall the following trigonometric identities.

This question tests one's ability to understand the connection between special triangles (30-60-90 and 45-45-90), trigonometric functions related to them (sine, cosine, tangent), and the corresponding degree/radian on the unit circle. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each  pair that lies on the circle can be found by creating a right triangle that has a base on the -axis and a hypotenuse that is from the center of the circle to the desired point on the edge of the circle. The height of the triangle is the vertical line that connects the point on the circle's edge to the -axis.

For the purpose of Common Core Standards, understanding "use special triangles to determine geometrically the values of sine, cosine, tangent for " , falls within the Cluster A of "extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF.TF.A).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Possible approaches to solving this problem:

I. Plot the angle on the unit circle to find the .

II. Identify the special triangle that corresponds to the angle.

III. Using memorization of the unit circle.

For this particular question let's us approach II.

Step 1: Simplify the angle if possible.

Step 2: Identify the special right triangle that corresponds to the angle.

Let's convert the angle to degrees to more easily see the special right triangle that it creates.

Therefore the special triangle that is created with  is 45-45-90 degree triangle. The angle which is made at the origin will be 45 degrees and the length of the segment from the origin to the edge of the unit circle is one by definition.

Step 3: Calculate the side lengths of the special triangle.

From here, recall that the special 45-45-90 degree triangle has the following side identities.

Step 4: Calculate cosine.

Recall the following trigonometric identities.

This question tests one's ability to understand the connection between special triangles (30-60-90 and 45-45-90), trigonometric functions related to them (sine, cosine, tangent), and the corresponding degree/radian on the unit circle. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each  pair that lies on the circle can be found by creating a right triangle that has a base on the -axis and a hypotenuse that is from the center of the circle to the desired point on the edge of the circle. The height of the triangle is the vertical line that connects the point on the circle's edge to the -axis.

For the purpose of Common Core Standards, understanding "use special triangles to determine geometrically the values of sine, cosine, tangent for " , falls within the Cluster A of "extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF.TF.A).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Possible approaches to solving this problem:

I. Plot the angle on the unit circle to find the .

II. Identify the special triangle that corresponds to the angle.

III. Using memorization of the unit circle.

For this particular question let's us approach II.

Step 1: Simplify the angle if possible.

Step 2: Identify the special right triangle that corresponds to the angle.

Let's convert the angle to degrees to more easily see the special right triangle that it creates.

Therefore the special triangle that is created with  is 45-45-90 degree triangle. The angle which is made at the origin will be 45 degrees and the length of the segment from the origin to the edge of the unit circle is one by definition.

Step 3: Calculate the side lengths of the special triangle.

From here, recall that the special 45-45-90 degree triangle has the following side identities.

Step 4: Calculate tangent.

Recall the following trigonometric identities.

Recall that when dividing fractions, one can multiply the numerator by the reciprocal of the denominator.

This question tests one's ability to understand the connection between special triangles (30-60-90 and 45-45-90), trigonometric functions related to them (sine, cosine, tangent), and the corresponding degree/radian on the unit circle. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each  pair that lies on the circle can be found by creating a right triangle that has a base on the -axis and a hypotenuse that is from the center of the circle to the desired point on the edge of the circle. The height of the triangle is the vertical line that connects the point on the circle's edge to the -axis.

For the purpose of Common Core Standards, understanding "use special triangles to determine geometrically the values of sine, cosine, tangent for " , falls within the Cluster A of "extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF.TF.A).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Possible approaches to solving this problem:

I. Plot the angle on the unit circle to find the .

II. Identify the special triangle that corresponds to the angle.

III. Using memorization of the unit circle.

For this particular question let's us approach II.

Step 1: Simplify the angle if possible.

Step 2: Identify the special right triangle that corresponds to the angle.

Let's convert the angle to degrees to more easily see the special right triangle that it creates.

Find the reference angle by subtracting the angle from from 180 degrees.

This means that 135 degrees is a 45 degree angle that lies in the second quadrant. Recall that the second quadrant contains positive  values and negative  values.

Therefore the special triangle that is created with  is 45-45-90 degree triangle. The angle which is made at the origin will be 45 degrees and the length of the segment from the origin to the edge of the unit circle is one by definition.

Step 3: Calculate the side lengths of the special triangle.

From here, recall that the special 45-45-90 degree triangle has the following side identities.

Step 4: Calculate tangent.

Recall the following trigonometric identities.

Since tangent represents the  values over the  values on the coordinate grid, this means that tangent is negative for angles in quadrant two.

This question tests one's ability to understand the connection between special triangles (30-60-90 and 45-45-90), trigonometric functions related to them (sine, cosine, tangent), and the corresponding degree/radian on the unit circle. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each  pair that lies on the circle can be found by creating a right triangle that has a base on the -axis and a hypotenuse that is from the center of the circle to the desired point on the edge of the circle. The height of the triangle is the vertical line that connects the point on the circle's edge to the -axis.

For the purpose of Common Core Standards, understanding "use special triangles to determine geometrically the values of sine, cosine, tangent for " , falls within the Cluster A of "extend the domain of trigonometric functions using the unit circle" concept (CCSS.MATH.CONTENT.HSF.TF.A).

Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.

Possible approaches to solving this problem:

I. Plot the angle on the unit circle to find the .

II. Identify the special triangle that corresponds to the angle.

III. Using memorization of the unit circle.

For this particular question let's us approach II.

Step 1: Simplify the angle if possible.

Step 2: Identify the special right triangle that corresponds to the angle.

Let's convert the angle to degrees to more easily see the special right triangle that it creates.

Find the reference angle by subtracting the angle from from 180 degrees.

This means that 135 degrees is a 45 degree angle that lies in the second quadrant. Recall that the second quadrant contains positive  values and negative  values.

Therefore the special triangle that is created with  is 45-45-90 degree triangle. The angle which is made at the origin will be 45 degrees and the length of the segment from the origin to the edge of the unit circle is one by definition.

Step 3: Calculate the side lengths of the special triangle.

From here, recall that the special 45-45-90 degree triangle has the following side identities.

Step 4: Calculate sine.

Recall the following trigonometric identities.

Since sine represents the  values on the coordinate grid, this means that sine remains positive for angles in quadrant two.