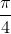All Common Core: High School - Functions Resources
Example Questions
Example Question #1 : Radians And Arc Length: Ccss.Math.Content.Hsf Tf.A.1
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.Math.content.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #2 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #3 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #4 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #5 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #6 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #7 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #8 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #9 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Example Question #1 : Trigonometric Functions
Convert 
This question tests one's ability to understand the conversion between radians and degrees. It relies on the understanding that the measure of an angle can be described using the properties of the unit circle and arc length. Furthermore, questions involving concepts dealing with trigonometry use the foundation of corresponding identities with angles that come from the unit circle. Recall that the unit circle is a circle that has a radius of one and is centered at the origin. Each 


For the purpose of Common Core Standards, understanding radian measure of an angle as the length of the arc on the unit circle subtended by the angle, falls within the Cluster A of extend the domain of trigonometric functions using the unit circle concept (CCSS.MATH.CONTENT.HSF.TF.A).
Knowing the standard and the concept for which it relates to, we can now do the step-by-step process to solve the problem in question.
Step 1: Identify the general formula for unit conversion between radians and degrees.
Therefore to convert from degrees to radian is,
Step 2: Identify the values given in the question.
Step 3: Substitute the value from step 2 into the formula from step 1.
The degree measurement in the numerator and denominator cancel out.
From here, simplify the fraction by finding common factors that exist in both the numerator and denominator.
Certified Tutor
Certified Tutor
All Common Core: High School - Functions Resources