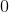We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Common Core: 8th Grade Math : Graph Proportional Relationships, Interpreting the Unit Rate as the Slope: CCSS.Math.Content.8.EE.B.5

Study concepts, example questions & explanations for Common Core: 8th Grade Math

Create An Account

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Other Lines

What is the slope of the line that passes through the points (3,4) $\displaystyle (3,4)$ and (5,13) $\displaystyle (5,13)$?

Possible Answers:

-4/3 $\displaystyle -4/3$

13/4 $\displaystyle 13/4$

-9/2 $\displaystyle -9/2$

2/9 $\displaystyle 2/9$

9/2 $\displaystyle 9/2$

Correct answer:

9/2 $\displaystyle 9/2$

Explanation:

The slope of a line is sometimes referred to as "rise over run." This is because the formula for slope is the change in y-value (rise) divided by the change in x-value (run). Therefore, if you are given two points, $(x_{1},y_{1})$ $\displaystyle (x_{1},y_{1})$ and $(x_{2},y_{2})$ $\displaystyle (x_{2},y_{2})$, the slope of their line can be found using the following formula: $slope=(y_{1}-y_{2})/(x_{1}-x_{2})$ $\displaystyle slope=(y_{1}-y_{2})/(x_{1}-x_{2})$

This gives us $\displaystyle (13-4)/(5-3)=9/2$.

Report an Error

Example Question #131 : Coordinate Geometry

Given points (1,2) $\displaystyle (1,2)$ and (-1,3) $\displaystyle (-1,3)$, what is the slope of the line connecting them?

Possible Answers:

$\displaystyle -1$

$-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$

$\frac{1}{2}$ $\displaystyle \frac{1}{2}$

$-\frac{1}{4}$ $\displaystyle -\frac{1}{4}$

$\displaystyle 1$

Correct answer:

$-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$

Explanation:

Write the slope formula. Plug in the points and solve.

$m= \frac{y_2-y_1}{x_2-x_1}= \frac{3-2}{-1-1}= -\frac{1}{2}$ $\displaystyle m= \frac{y_2-y_1}{x_2-x_1}= \frac{3-2}{-1-1}= -\frac{1}{2}$

Report an Error

Example Question #2 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

What is the slope of the line connecting the points $(2,\sqrt2)$ $\displaystyle (2,\sqrt2)$ and (1,2) $\displaystyle (1,2)$?

Possible Answers:

$-\sqrt2-2$ $\displaystyle -\sqrt2-2$

$-1-\sqrt2$ $\displaystyle -1-\sqrt2$

$-\sqrt2+1$ $\displaystyle -\sqrt2+1$

$2-\sqrt2$ $\displaystyle 2-\sqrt2$

$\sqrt2 -2$ $\displaystyle \sqrt2 -2$

Correct answer:

$\sqrt2 -2$ $\displaystyle \sqrt2 -2$

Explanation:

Write the slope formula. Plug in the point, and simplify.

$m=\frac{y_2-y_1}{x_2-x_1}= \frac{2-\sqrt2}{1-2}=\frac{2-\sqrt2}{-1}= -(2-\sqrt2) = \sqrt2-2$ $\displaystyle m=\frac{y_2-y_1}{x_2-x_1}= \frac{2-\sqrt2}{1-2}=\frac{2-\sqrt2}{-1}= -(2-\sqrt2) = \sqrt2-2$

Report an Error

Example Question #132 : Coordinate Geometry

What is the slope of a line with an $\displaystyle x$-intercept is $\displaystyle 4$ and another $\displaystyle x$-intercept of $\displaystyle 6$?

Possible Answers:

$\displaystyle 4$

$\displaystyle 6$

$\displaystyle 5$

$\infty$ $\displaystyle \infty$

$\displaystyle 0$

Correct answer:

$\displaystyle 0$

Explanation:

The $\displaystyle x$-intercept is the $\displaystyle x$ value when y=0 $\displaystyle y=0$.

Therefore, since the two $\displaystyle x$-intercepts are $\displaystyle 4$ and $\displaystyle 6$, the points are (4,0) $\displaystyle (4,0)$ and (6,0) $\displaystyle (6,0)$.

Write the slope formula, plug in the values, and solve.

$m=\frac{y_2-y_1}{x_2-x_1} = \frac{0-0}{6-4}= \frac{0}{2} =0$ $\displaystyle m=\frac{y_2-y_1}{x_2-x_1} = \frac{0-0}{6-4}= \frac{0}{2} =0$

The slope is zero.

Report an Error

Example Question #4 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Given the points (4, 3) $\displaystyle (4, 3)$ and (8, 9) $\displaystyle (8, 9)$, find the slope of the line.

Possible Answers:

$\frac{4}{3}$ $\displaystyle \frac{4}{3}$

$\frac{2}{3}$ $\displaystyle \frac{2}{3}$

$\frac{-6}{4}$ $\displaystyle \frac{-6}{4}$

$\frac{-3}{4}$ $\displaystyle \frac{-3}{4}$

$\frac{3}{2}$ $\displaystyle \frac{3}{2}$

Correct answer:

$\frac{3}{2}$ $\displaystyle \frac{3}{2}$

Explanation:

The formula for the slope of a line is $\frac{y_2-y_1}{x_2-x_1}$ $\displaystyle \frac{y_2-y_1}{x_2-x_1}$.

We then plug in the points given: $\frac{9-3}{8-4}=\frac{6}{4}$ $\displaystyle \frac{9-3}{8-4}=\frac{6}{4}$ which is then reduced to $\frac{3}{2}$ $\displaystyle \frac{3}{2}$.

Report an Error

Example Question #5 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

A line crosses the x-axis at (6,8) $\displaystyle (6,8)$ and the y-axis at (0,6) $\displaystyle (0,6)$. What is the slope of this line?

Possible Answers:

$m=\frac{1}{3}$ $\displaystyle m=\frac{1}{3}$

$m=-\frac{1}{3}$ $\displaystyle m=-\frac{1}{3}$

None of these.

m=-3 $\displaystyle m=-3$

m=3 $\displaystyle m=3$

Correct answer:

$m=\frac{1}{3}$ $\displaystyle m=\frac{1}{3}$

Explanation:

Given the points,

$\$x_1,y_1)=(0,6) \\(x_2,y_2)=(6,8)$ \(\displaystyle \\(x_1,y_1)=(0,6) \\(x_2,y_2)=(6,8)$.

We compute slope (m) as follows:

$m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{8-6}{6-0}=\mathbf{\frac{1}{3}}$ $\displaystyle m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{8-6}{6-0}=\mathbf{\frac{1}{3}}$

Report an Error

Example Question #6 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Find the slope of the line that passes through the points:

(12, 2) $\displaystyle (12, 2)$ and $\displaystyle (-12, 4)$

Possible Answers:

$-\frac{3}{4}$ $\displaystyle -\frac{3}{4}$

$-\frac{1}{12}$ $\displaystyle -\frac{1}{12}$

$\displaystyle -8$

$\displaystyle 12$

Correct answer:

$-\frac{1}{12}$ $\displaystyle -\frac{1}{12}$

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$ $\displaystyle \text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{4-2}{-12-12}$ $\displaystyle \text{Slope}=\frac{4-2}{-12-12}$

Simplify.

$\text{Slope}=\frac{2}{-24}$ $\displaystyle \text{Slope}=\frac{2}{-24}$

Solve.

$\text{Slope}=-\frac{1}{12}$ $\displaystyle \text{Slope}=-\frac{1}{12}$

Report an Error

Example Question #1 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Find the slope of the line that passes through the points:

(2, 4) $\displaystyle (2, 4)$ and $\displaystyle (-10, -20)$

Possible Answers:

$-\frac{1}{2}$ $\displaystyle -\frac{1}{2}$

$\frac{7}{8}$ $\displaystyle \frac{7}{8}$

$\displaystyle 2$

$\displaystyle 4$

Correct answer:

$\displaystyle 2$

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$ $\displaystyle \text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{-20-4}{-10-2}$ $\displaystyle \text{Slope}=\frac{-20-4}{-10-2}$

Simplify.

$\text{Slope}=\frac{-24}{-12}$ $\displaystyle \text{Slope}=\frac{-24}{-12}$

Solve.

$\text{Slope}=2$ $\displaystyle \text{Slope}=2$

Report an Error

Example Question #62 : Other Lines

Find the slope of the line that passes through the points:

(4, 5) $\displaystyle (4, 5)$ and (-3, 1) $\displaystyle (-3, 1)$

Possible Answers:

$\frac{5}{7}$ $\displaystyle \frac{5}{7}$

$-\frac{2}{7}$ $\displaystyle -\frac{2}{7}$

$\frac{3}{7}$ $\displaystyle \frac{3}{7}$

$\frac{4}{7}$ $\displaystyle \frac{4}{7}$

Correct answer:

$\frac{4}{7}$ $\displaystyle \frac{4}{7}$

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$ $\displaystyle \text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{1-5}{-3-4}$ $\displaystyle \text{Slope}=\frac{1-5}{-3-4}$

Simplify.

$\text{Slope}=\frac{-4}{-7}$ $\displaystyle \text{Slope}=\frac{-4}{-7}$

Solve.

$\text{Slope}=\frac{4}{7}$ $\displaystyle \text{Slope}=\frac{4}{7}$

Report an Error

Example Question #71 : Other Lines

Find the slope of the line that passes through the points:

(8, 15) $\displaystyle (8, 15)$ and $\displaystyle (-39, 13)$

Possible Answers:

$-\frac{34}{47}$ $\displaystyle -\frac{34}{47}$

$\frac{2}{47}$ $\displaystyle \frac{2}{47}$

$\frac{12}{47}$ $\displaystyle \frac{12}{47}$

$\frac{19}{4}$ $\displaystyle \frac{19}{4}$

Correct answer:

$\frac{2}{47}$ $\displaystyle \frac{2}{47}$

Explanation:

Recall that the slope of a line also measures how steep the line is. Use the following equation to find the slope of the line:

$\text{Slope}=\frac{y_2-y_1}{x_2-x_1}$ $\displaystyle \text{Slope}=\frac{y_2-y_1}{x_2-x_1}$

Now, substitute in the information using the given points.

$\text{Slope}=\frac{13-15}{-39-8}$ $\displaystyle \text{Slope}=\frac{13-15}{-39-8}$

Simplify.

$\text{Slope}=\frac{-2}{-47}$ $\displaystyle \text{Slope}=\frac{-2}{-47}$

Solve.

$\text{Slope}=\frac{2}{47}$ $\displaystyle \text{Slope}=\frac{2}{47}$

Report an Error

View Tutors

David
Certified Tutor

Kent State University, Bachelors, Marketing. Kent State University at Kent, Masters in Education, Special Education.

View Tutors

Andy
Certified Tutor

The University of Texas at Dallas, Bachelors, Interdisciplinary Studies .

View Tutors

Rainier
Certified Tutor

Norfolk State University, Bachelors, Physics.

All Common Core: 8th Grade Math Resources

7 Diagnostic Tests 75 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

MCAT Tutors in San Francisco-Bay Area, Chemistry Tutors in New York City, LSAT Tutors in Houston, Calculus Tutors in Dallas Fort Worth, Reading Tutors in Phoenix, English Tutors in Los Angeles, ACT Tutors in Dallas Fort Worth, Calculus Tutors in Houston, LSAT Tutors in San Francisco-Bay Area, SSAT Tutors in Philadelphia

Popular Courses & Classes

LSAT Courses & Classes in Miami, LSAT Courses & Classes in Los Angeles, MCAT Courses & Classes in Chicago, GRE Courses & Classes in Boston, MCAT Courses & Classes in Boston, LSAT Courses & Classes in San Diego, SSAT Courses & Classes in Denver, LSAT Courses & Classes in Denver, GMAT Courses & Classes in Philadelphia, Spanish Courses & Classes in Boston

Popular Test Prep

ACT Test Prep in Washington DC, ISEE Test Prep in New York City, MCAT Test Prep in Chicago, ISEE Test Prep in Washington DC, SAT Test Prep in Houston, SSAT Test Prep in Denver, LSAT Test Prep in Boston, GRE Test Prep in Boston, MCAT Test Prep in Phoenix, MCAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Common Core: 8th Grade Math : Graph Proportional Relationships, Interpreting the Unit Rate as the Slope: CCSS.Math.Content.8.EE.B.5

Study concepts, example questions & explanations for Common Core: 8th Grade Math

All Common Core: 8th Grade Math Resources

Example Questions

Example Question #61 : Other Lines

Example Question #131 : Coordinate Geometry

Example Question #2 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #132 : Coordinate Geometry

Example Question #4 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #5 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #6 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #1 : Graph Proportional Relationships, Interpreting The Unit Rate As The Slope: Ccss.Math.Content.8.Ee.B.5

Example Question #62 : Other Lines

Example Question #71 : Other Lines

All Common Core: 8th Grade Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: