All Common Core: 8th Grade Math Resources
Example Questions
Example Question #1 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Solve the rational equation:

no solution
no solution
With rational equations we must first note the domain, which is all real numbers except 










Example Question #1 : How To Find Out When An Equation Has No Solution
How many solutions does the equation below have?
One
No solutions
Two
Three
Infinite
No solutions
When finding how many solutions an equation has you need to look at the constants and coefficients.
The coefficients are the numbers alongside the variables.
The constants are the numbers alone with no variables.
If the coefficients are the same on both sides then the sides will not equal, therefore no solutions will occur.
Use distributive property on the right side first.

No solutions
Example Question #2 : How To Find Out When An Equation Has No Solution
Solve:
First factorize the numerator.
Rewrite the equation.
The 
Subtract one on both sides.
However, let's substitute this answer back to the original equation to check whether if we will get 
Simplify the left side.
The left side does not satisfy the equation because the fraction cannot be divided by zero.
Therefore, 
The answer is:
Example Question #3 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Solve for 
No solution
No solution
Combine like terms on each side of the equation:
Next, subtract 
Then subtract 
This is nonsensical; therefore, there is no solution to the equation.
Example Question #3 : How To Find Out When An Equation Has No Solution
Solve the equation:
No solution
No solution
Notice that the end value is a negative. Any negative or positive value that is inside an absolute value sign must result to a positive value.
If we split the equation to its positive and negative solutions, we have:
Solve the first equation.
The answer to 
Solve the second equation.
The answer to 

If we substitute these two solutions back to the original equation, the results are positive answers and can never be equal to negative one.
The answer is no solution.
Example Question #1 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Select the option that describes the solution(s) for the following equation:
No solution
Infinitely many solutions
One solution
No solution
Let's begin by discussing our answer choices:
In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,
In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,
In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example, 
To answer this question, we can solve the equation:
This equation equals a false statement; thus, the correct answer is no solution.
Example Question #7 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Select the option that describes the solution(s) for the following equation:
Infinitely many solutions
One solution
No solution
No solution
Let's begin by discussing our answer choices:
In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,
In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,
In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example, 
To answer this question, we can solve the equation:
This equation equals a false statement; thus, the correct answer is no solution.
Example Question #1 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Select the option that describes the solution(s) for the following equation:
One solution
Infinitely many solutions
No solution
No solution
Let's begin by discussing our answer choices:
In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,
In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,
In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example, 
To answer this question, we can solve the equation:
This equation equals a false statement; thus, the correct answer is no solution.
Example Question #1 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Select the option that describes the solution(s) for the following equation:
Infinitely many solutions
One solution
No solution
No solution
Let's begin by discussing our answer choices:
In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,
In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,
In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example, 
To answer this question, we can solve the equation:
This equation equals a false statement; thus, the correct answer is no solution.
Example Question #2 : Give Examples Of Linear Equations: Ccss.Math.Content.8.Ee.C.7a
Select the option that describes the solution(s) for the following equation:
One solution
Infinitely many solutions
No solution
Infinitely many solutions
Let's begin by discussing our answer choices:
In order for an equation to have no solution, the equation, when solved, must equal a false statement; for example,
In order for an equation to have one solution, the equation, when solved for a variable, but equal a single value; for example,
In order for an equation to have infinitely many solutions, the equation, when solved, must equal a statement that is always true; for example, 
To answer this question, we can solve the equation:
This equation equals a statement that is always true; thus, the correct answer is infinitely many solutions.
All Common Core: 8th Grade Math Resources












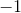

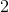



































![\frac{\begin{array}[b]{r}2x=2x+5\\ -2x -2x\ \ \ \ \ \end{array}}{0=5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/950973/gif.latex)



![\frac{\begin{array}[b]{r}13y=13y-17\\ -13y -13y \ \ \ \ \ \ \end{array}}{0=-17}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/951210/gif.latex)



![\frac{\begin{array}[b]{r}9x=9x+27\\ -9x -9x\ \ \ \ \ \ \ \end{array}}{0=27}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/951172/gif.latex)



![\frac{\begin{array}[b]{r}43x=43x-34\\ -43x -43x\ \ \ \ \ \ \end{array}}{0=-34}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/951300/gif.latex)








