All Common Core: 8th Grade Math Resources
Example Questions
Example Question #31 : Geometric Translations
Observe the location of the black and orange parallel lines on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black lines have undergone in order to reach the position of the orange lines. Select the answer that provides the correct transformation shown in the provided image.

A reflection over the y-axis
A 
A translation down
A 
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, notice that the lines made a rotation to the right around the x-axis, and the rotation was 

The transformation can't be a reflection over the y-axis because the orange lines didn't flip over the y-axis.
The transformation can't be a translation because the lines changed direction, which does not happened when you simply move or slide a line or image.
Example Question #343 : Grade 8
Observe the location of the black and orange parallel lines on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black lines have undergone in order to reach the position of the orange lines. Select the answer that provides the correct transformation shown in the provided image.

A translation to the left
Reflection over the x-axis
A 
Reflection over the x-axis
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, the lines were not rotated 
Example Question #8 : Parallel Lines: Ccss.Math.Content.8.G.A.1c
Observe the location of the black and orange parallel lines on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black lines have undergone in order to reach the position of the orange lines. Select the answer that provides the correct transformation shown in the provided image.

A 
Translation down
Reflection over the y-axis
Translation down
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, the lines were not rotated 
Example Question #1 : Parallel Lines: Ccss.Math.Content.8.G.A.1c
Observe the location of the black and orange parallel lines on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black lines have undergone in order to reach the position of the orange lines. Select the answer that provides the correct transformation shown in the provided image.

A translation to the left
Reflection over the x-axis
A 
Reflection over the x-axis
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, the lines were not rotated 

Example Question #344 : Grade 8
Observe the location of the black and orange parallel lines on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black lines have undergone in order to reach the position of the orange lines. Select the answer that provides the correct transformation shown in the provided image.

Reflection over the y-axis
A 
Translation down
Translation down
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, the lines were not rotated 
Example Question #31 : Geometry
Observe the location of the black and orange parallel lines on the provided coordinate plane and identify which of the following transformations—rotation, translation, or reflection—the black lines have undergone in order to reach the position of the orange lines. Select the answer that provides the correct transformation shown in the provided image.
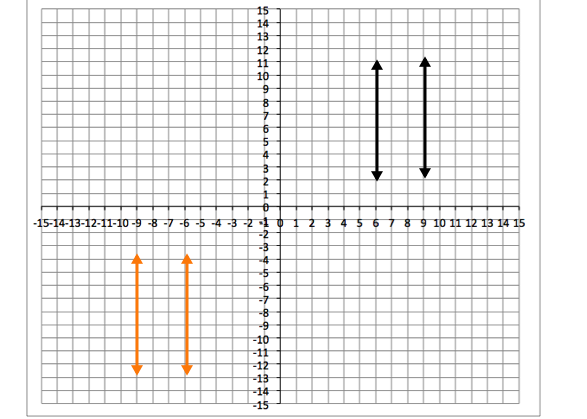
A reflection over the y-axis
A translation down and to the left
A 
A translation down and to the left
First, let's define the possible transformations.
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
In the images from the question, the lines were not rotated 
Example Question #1 : Understand Congruency Of Two Dimensional Figures: Ccss.Math.Content.8.G.A.2
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, translation down
Yes, a reflection over the x-axis
No
Yes, a 
Yes, a reflection over the x-axis
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are the same size; thus, the triangles are congruent. The red triangle has been flipped; thus, the triangle has been reflected over the x-axis.
The triangle has not undergone a translation, because a translation would have only moved the triangle, not flipped it. Also, the triangle has not been rotated 
Example Question #1 : Understand Congruency Of Two Dimensional Figures: Ccss.Math.Content.8.G.A.2
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, translation to the left
Yes, reflection over the x-axis
No
Yes, rotation
Yes, rotation
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are the same size; thus, the triangles are congruent. The red triangle has been rotated 
The triangle has not undergone a translation, because a translation would have only moved the triangle, not rotated. Also, the triangle has not been reflected over the x-axis because it doesn't flip over the x-axis.
Example Question #2 : Understand Congruency Of Two Dimensional Figures: Ccss.Math.Content.8.G.A.2
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, reflected over the y-axis
Yes, rotated
No
Yes, translation down
Yes, rotated
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are the same size; thus, the triangles are congruent. The red triangle has been rotated 
The triangle has not undergone a translation, because a translation would have only moved the triangle, not flipped or rotated it. The red triangle has not been flipped over the y-axis; thus, the triangle has not been reflected over the y-axis.
Example Question #1 : Understand Congruency Of Two Dimensional Figures: Ccss.Math.Content.8.G.A.2
Are the two shapes shown in the coordinate plane congruent? If so, what transformation did the red shape undergo from the orange shape?

Yes, 
Yes, translation to the right
Yes, reflection over the y-axis
No
Yes, reflection over the y-axis
In order to solve this problem, we first need to know what "congruent" means. For two shapes to be congruent, they need to be the same shape and the same size. The shape can go through a transformation—rotation, translation, or reflection—but nothing else about the original shape can be changed for two shapes to be congruent.
Also, let's recall the types of transformations:
Rotation: A rotation means turning an image, shape, line, etc. around a central point.
Translation: A translation means moving or sliding an image, shape, line, etc. over a plane.
Reflection: A reflection mean flipping an image, shape, line, etc. over a central line.
For this question, we can tell that the triangles are the same size; thus, the triangles are congruent. The red triangle has been flipped; thus, the triangle has been reflected over the y-axis.
The triangle has not undergone a translation, because a translation described would have only moved the triangle to the right, not to the left. Also, the triangle has not been rotated 
All Common Core: 8th Grade Math Resources






