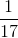All Common Core: 7th Grade Math Resources
Example Questions
Example Question #152 : Statistics & Probability
Dan has a bag of 





Dan starts out with 

Now that Dan has taken a yellow marble from the bag, we still have 

Example Question #153 : Statistics & Probability
Dan has a bag of 





Dan starts out with 

Now that Dan has taken an orange marble from the bag, we still have 

Example Question #154 : Statistics & Probability
Dan has a bag of 





Dan starts out with 

Now that Dan has taken an orange marble from the bag, we have 

Example Question #155 : Statistics & Probability
Dan has a bag of 





Dan starts out with 

Now that Dan has taken a blue marble from the bag, we have 

Example Question #11 : Understand Fraction Of Outcomes: Ccss.Math.Content.7.Sp.C.8a
Dan has a bag of 





Dan starts out with 

Now that Dan has taken a red marble from the bag, we have 

Example Question #1 : Represent Sample Spaces For Compound Events: Ccss.Math.Content.7.Sp.C.8b
Charlie is going to roll a die and flip a coin. What is the probability that he will roll a 
To help us solve this problem, we can make a tree diagram to show all of the possible outcomes of rolling a die and flipping a coin:

As shown from the diagram, we have 

Example Question #2 : Represent Sample Spaces For Compound Events: Ccss.Math.Content.7.Sp.C.8b
Charlie is going to roll a die and flip a coin. What is the probability that he will roll a 
To help us solve this problem, we can make a tree diagram to show all of the possible outcomes of rolling a die and flipping a coin:

As shown from the diagram, we have 

Example Question #1 : Represent Sample Spaces For Compound Events: Ccss.Math.Content.7.Sp.C.8b
Charlie is going to roll a die and flip a coin. What is the probability that he will roll an even number and the coin will land with heads facing up?
To help us solve this problem, we can make a tree diagram to show all of the possible outcomes of rolling a die and flipping a coin:

As shown from the diagram, we have 



Example Question #2 : Represent Sample Spaces For Compound Events: Ccss.Math.Content.7.Sp.C.8b
Charlie is going to roll a die and flip a coin. What is the probability that he will roll an odd number and the coin will land with tails facing up?
To help us solve this problem, we can make a tree diagram to show all of the possible outcomes of rolling a die and flipping a coin:

As shown from the diagram, we have 



Example Question #5 : Represent Sample Spaces For Compound Events: Ccss.Math.Content.7.Sp.C.8b
Charlie is going to roll a die and flip a coin. What is the probability that he will roll a 
To help us solve this problem, we can make a tree diagram to show all of the possible outcomes of rolling a die and flipping a coin:

As shown from the diagram, we have 

Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources