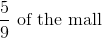All Common Core: 7th Grade Math Resources
Example Questions
Example Question #21 : Proportion / Ratio / Rate
On a map, 

Set up the following proportion:

where 
Now, solve for 
The two cities are 
Example Question #22 : Proportion / Ratio / Rate
Chuck is building a driveway that measures 


First, find the area of the driveway.
Since it takes 

Example Question #21 : Rational Numbers
Joanna can finish 


First, find out how long it will take her to finish 
Since it takes Joanna 
It will take her 

Example Question #11 : Ratios & Proportional Relationships
A car travels 

Divide the number of miles by the number of hours to get the number of miles per hour.
Example Question #12 : Ratios & Proportional Relationships
Joe used 

The phrase "bags of oranges does he use per gallon" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have bags of oranges, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Joe will use 
Example Question #13 : Ratios & Proportional Relationships
A landscaper can mow 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have yards, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
The landscaper can mow 
Example Question #14 : Ratios & Proportional Relationships
Hannah loves to shop. She can shop in 

The phrase "per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have the portion of the mall, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Hannah can shop in 
Example Question #11 : Grade 7
Charlie walks 


The phrase "miles per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have miles, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Charlie can walk at a speed of:
Example Question #12 : Grade 7
Alan walks 


The phrase "miles per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have miles, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Alan can walk at a speed of:
Example Question #16 : Ratios & Proportional Relationships
Jake walks 


The phrase "miles per hour" gives us a clue that we are going to divide. In this problem, we can replace the word "per" with a division sign; therefore, we will have miles, 

Remember that when we divide fractions, we can simply multiply by the reciprocal of the denominator to solve.
Therefore:
Jake can walk at a speed of:
Certified Tutor
Certified Tutor
All Common Core: 7th Grade Math Resources