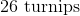All Common Core: 6th Grade Math Resources
Example Questions
Example Question #51 : Ratios & Proportional Relationships
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #61 : How To Find The Solution To An Equation
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #1 : Solve Unit Rate Problems: Ccss.Math.Content.6.Rp.A.3b
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #62 : How To Find The Solution To An Equation
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #51 : Grade 6
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #61 : How To Find The Solution To An Equation
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #52 : Grade 6
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #53 : Grade 6
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #74 : How To Find A Ratio
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Example Question #732 : Ssat Middle Level Quantitative (Math)
At a local market, farmers trade produce to obtain a more diverse crop. A farmer will trade 


Ratios can be written in the following format:
Using this format, substitute the given information to create a ratio.
Rewrite the ratio as a fraction.
We know that the farmer has 

Create a proportion using the two ratios.
Cross multiply and solve for 
Simplify.
Divide both sides of the equation by 
Solve.
The farmer can get 
Certified Tutor
Certified Tutor
All Common Core: 6th Grade Math Resources