All College Algebra Resources
Example Questions
Example Question #73 : Solving Equations And Inequallities
Solve
In order to solve this, we need to figure out what values of x makes the numerator and denominator equal zero.
These values are 

Then test a few numbers greater or lesser than the above values to figure out what range of values make the inequality true.
Example Question #2 : Rational Inequalities
Give the solution set of the equation
The boundary points of a rational inequality are the zeroes of the numerator and the denominator.
First, set the numerator equal to 0 and solve for 
Now set the denominator equal to 0 and solve for 
Factor the trinomial using the reverse-FOIL method. Look for two integers whose sum is 


Set each factor to zero and solve for 
Therefore, the boundary points are 

The four intervals are listed below, along with their arbitrary test points.

True; include 

False; exclude 


True; include


False; exclude 
Since the inequality symbol is the "is greater than or equal to" symbol, include the zero, 0, of the numerator - but not the other two boundaries, the zeroes of the denominator. This makes the solution set
![(-\infty, 0] \cup (1,7)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970383/gif.latex)
Certified Tutor
Certified Tutor
All College Algebra Resources



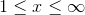
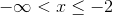


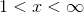





![(-\infty, 0] \cup [1,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970293/gif.latex)
![(-\infty, 0] \cup (1,7)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970292/gif.latex)


![[0,1]\cup [7, \infty)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/970294/gif.latex)
































