All College Algebra Resources
Example Questions
Example Question #61 : Polynomial Functions
Consider the polynomial

Going by Descartes' Rule of Signs alone, how many positive real zeroes could the polynomial have?
One or three
Exactly three
Exactly two
None or two
Exactly one
None or two
By Descartes' Rule of Signs, the number of positive real zeroes of a polynomial 
This means that this polynomial must have either zero or two such zeroes.
Example Question #1 : Transformations Of Parabolic Functions
If the function 

Example Question #251 : New Sat
Which of the following graphs correctly represents the quadratic inequality below (solutions to the inequalities are shaded in blue)?






To begin, we analyze the equation given: the base equation, 


To solve the inequality, we need to take a test point and plug it in to see if it matches the inequality. The only points that cannot be used are those directly on our parabola, so let's use the origin 
Simplified as:
Which is not true, so the area inside of the parabola should be shaded, resulting in the following graph:

Example Question #1 : Graphing Polynomials
How many zeroes does the following polynomial have?







If we try the next number up, 3, we get this:


and now we need to see if 
There aren't any real numbers that square to get -5 so this has no roots. Thus, 
Example Question #64 : Polynomial Functions



True or false: By the Intermediate Value Theorem, 

True
False
False
As a polynomial function, the graph of 




Set 





Both are polynomial graphs fitting the given conditions, but the only the equation graphed at right has a zero on 
Example Question #61 : Polynomial Functions
True or false:
The polynomial 

False
True
True
One way to answer this question is as follows:
Let 



as its coefficient sum, so 

Example Question #5 : Graphing Polynomials
True or false:
The polynomial 

False
True
False
Let 


To find this alternating sum, it is necessary to reverse the symbol before all terms of odd degree. In 


so 

Example Question #66 : Polynomial Functions



True or false: By the Intermediate Value Theorem, 

True
False
True
As a polynomial function, the graph of 




Setting 








Example Question #7 : Graphing Polynomials
Let 

True or false: It follows that 

True
False
True
By the Factor Theorem, 













Example Question #21 : Graphing Functions
Which of the following graphs matches the function 


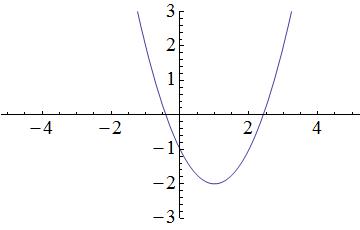



Start by visualizing the graph associated with the function :

Terms within the parentheses associated with the squared x-variable will shift the parabola horizontally, while terms outside of the parentheses will shift the parabola vertically. In the provided equation, 2 is located outside of the parentheses and is subtracted from the terms located within the parentheses; therefore, the parabola in the graph will shift down by 2 units. A simplified graph of looks like this:

Remember that there is also a term within the parentheses. Within the parentheses, 1 is subtracted from the x-variable; thus, the parabola in the graph will shift to the right by 1 unit. As a result, the following graph matches the given function :

All College Algebra Resources


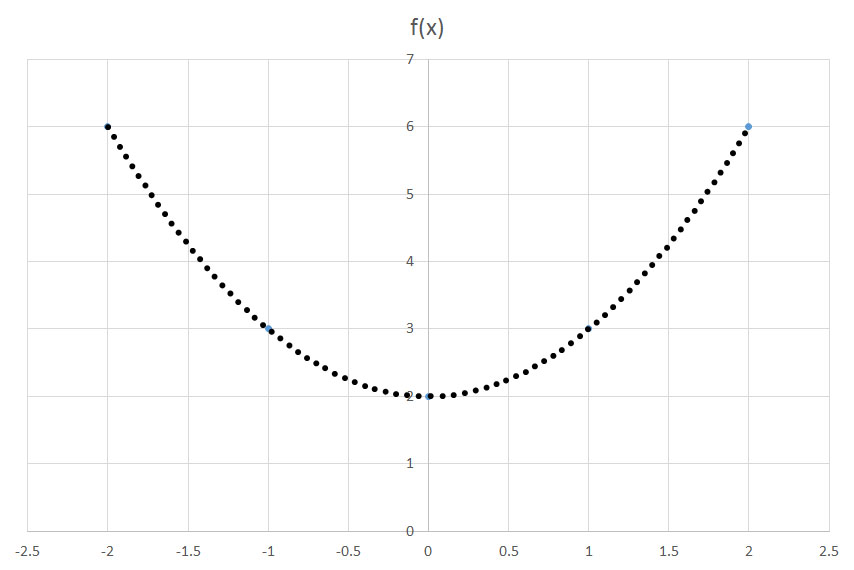



 shifts a function f(x)
shifts a function f(x)  units to the left. Conversely,
units to the left. Conversely,  shifts a function f(x)
shifts a function f(x)  units to the right. In this question, we are translating the graph two units to the left.
units to the right. In this question, we are translating the graph two units to the left. or
or  .
.













