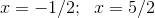All College Algebra Resources
Example Questions
Example Question #5 : Symmetry

The above table refers to a function 

Is this function even, odd, or neither?
Odd
Neither
Even
Neither
A function 




We see that 





For a function to be odd, since 





The correct choice is neither.
Example Question #4 : Symmetry
Define 
Is this function even, odd, or neither?
Even
Odd
Neither
Neither
A function 













Example Question #7 : Symmetry

How can 






One implication of this is that for 


for nonnegative values, then, by substitution,
This condition is satisfied.
Now, if 


so for all

the correct response.
Example Question #5 : Symmetry

Consider the relation graphed above. Which is true of this relation?
The relation is an even function.
The relation is an odd function.
The relation not a function.
The relation is a function which is neither even nor odd.
The relation is a function which is neither even nor odd.
The relation passes the Vertical Line test, as seen in the diagram below, in that no vertical line can be drawn that intersects the graph than once:

An function is odd if and only if its graph is symmetric about the origin, and even if and only if its graph is symmetric about the 
Example Question #9 : Symmetry

How can 





One implication of this is that for 


Now, if 


so for all
This is the correct choice.
Example Question #10 : Symmetry
Which of the following is symmetrical to 
Symmetry across the origin is symmetry across 
Determine the inverse of the function. Swap the x and y variables, and solve for y.
Subtract 3 on both sides.
Divide by negative two on both sides.
The answer is:
Example Question #154 : College Algebra
Consider the function 
Is 
Neither
Odd
Even
Even
A function 


It is odd if, for each 

Substitute 

Since 

Example Question #72 : Graphs


Is 
Even
Neither
Odd
Odd
A function 


It is odd if, for each 

Substitute 


Since 

This makes 
Example Question #1 : Rational Functions
Find all horizontal and vertical asymptotes in the graph of 
Horizontal asymptote at y=0
Vertical asymptote at x=-3
None of these.
Horizontal asymptote at x=0
Vertical asymptote at y=3
Horizontal asymptote at y=1
Vertical asymptote at x=3
Horizontal asymptote at y=1
Vertical asymptote at x=0
Horizontal asymptote at y=1
Vertical asymptote at x=3
To find vertical asymptotes, factor each quadratic and then simplify.
The vertical asymptotes are the zeros of the denominator, so x=3 is a vertical asymptote.
Horizontal asymptotes are found by analyzing the coefficients of the first term in each equation. The line 
Example Question #1 : Rational Functions
Where are the vertical asymptotes of this rational function?
the function has no vertical asymptotes.
The vertical asymptotes of a rational function are always the zeroes of the polynomial in the denominator. So to solve this problem all we need to do is find the zeroes of 
We can use the quadratic formula, 

And we get the two roots, 
Certified Tutor
Certified Tutor
All College Algebra Resources













![f(x) = -[(-x)^{4}+ (-x)^{3}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/966438/gif.latex)







![f(x) = - \ln[ (-x)^2+(-x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/966459/gif.latex)