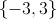When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle -6+4i+(5+5i)=-6+4i+5+5i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle -6+4i+5+5i=(-6+5)+(4i+5i)\)

\(\displaystyle (-6+5)+(4i+5i)=-1+9i\)

This gives a final answer of -1+9i

When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle -2+3i-(-6+4i)=-2+3i+6-4i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle -2+3i+6-4i=(-2+6)+(3i-4i)\)

\(\displaystyle (-2+6)+(3i-4i)=4-i\)

This gives a final answer of 10-4i

When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle -6+12i+(-2-3i)=-6+12i-2-3i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle -6+12i-2-3i=(-6-2)+(12i-3i)\)

\(\displaystyle (-6-2)+(12i-3i)=-8+9i\)

This gives a final answer of -8+9i

When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle 5-2i+(4-3i)=5-2i+4-3i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle 5-2i+4-3i=(5+4)+(-2i-3i)\)

\(\displaystyle (5+4)+(-2i-3i)=9-5i\)

This gives a final answer of 9-5i

When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle 11+3i+(-2+6i)=11+3i-2+6i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle 11+3i-2+6i=(11-2)+(3i+6i)\)

\(\displaystyle (11-2)+(3i+6i)=9+9i\)

This gives a final answer of 9+9i

When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle 6-5i-(-12-4i)=6-5i+12+4i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle 6-5i+12+4i=(6+12)+(-5i+4i)\)

\(\displaystyle (6+12)+(-5i+4i)=18-i\)

This gives a final answer of 18-i

When simplifying expressions with complex numbers, use the same techniques and procedures as normal. 

Distribute the sign to the terms in parentheses:

\(\displaystyle 16-3i-(12-2i)=16-3i-12+2i\)

Combine like terms- combine the real numbers together and the imaginary numbers together:

\(\displaystyle 16-3i-12+2i=(16-12)+(-3i+2i)\)

\(\displaystyle (16-12)+(-3i+2i)=4-i\)

This gives a final answer of 4-i

\(\displaystyle \frac{3+3i}{5-3i}\)

Multiply ply by the conjugate:

\(\displaystyle \frac{3+3i}{5-3i}\times \frac{5+3i}{5+3i}=\frac{15+9i+15i+9i^2}{25-9i^2}\)

Simplify:

\(\displaystyle \frac{15+9i+15i+9i^2}{25-9i^2}=\frac{6+24i}{34}\rightarrow \boldsymbol{\frac{6}{34}+\frac{12i}{17}}\)

\(\displaystyle \frac{2}{1+i}-\frac{3}{1-i}\)

Find a common denominator and subtract.

To do so multiply the numerator and denominator of both fractions by the denominator of the opposite fraction:

\(\displaystyle \frac{2(1-i)}{1+i(1-i)}-\frac{3(1+i)}{1-i(1+i)}\)

Combine and simplify:

\(\displaystyle \frac{2-2i-3-3i}{1-i^2}\rightarrow \frac{-1-5i}{2}\rightarrow \boldsymbol{\frac{-1}{2}-\frac{5}{2}i}\)

Keep in mind 

\(\displaystyle i^2=-1\)

By substituting \(\displaystyle u = x^{2}\) - and, subsequently, \(\displaystyle u^{2} =\left ( x^{2} \right )^{2} = x^{4}\) this can be rewritten as a quadratic equation, and solved as such:

\(\displaystyle x^{4} +5x^{2} - 36 = 0\)

\(\displaystyle u^{2} + 5u - 36 = 0\)

We are looking to factor the quadratic expression as \(\displaystyle (u+?)(u+?)\), replacing the two question marks with integers with product \(\displaystyle -36\) and sum 5; these integers are \(\displaystyle 9,-4\).

\(\displaystyle (u+9)(u-4) = 0\)

Substitute back:

\(\displaystyle (x^{2}+9)(x^{2}-4) = 0\)

The first factor cannot be factored further. The second factor, however, can itself be factored as the difference of squares:

\(\displaystyle (x^{2}+9)(x+2)(x-2) = 0\)

Set each factor to zero and solve:

\(\displaystyle x^{2}+9= 0\) 

\(\displaystyle x^{2}= -9\)

Since no real number squared is equal to a negative number, no real solution presents itself here. 

\(\displaystyle x-2= 0 \Rightarrow x = 2\)

\(\displaystyle x+2 = 0 \Rightarrow x = - 2\)

The solution set is \(\displaystyle \left \{ -2, 2\right \}\).