All Calculus AB Resources
Example Questions
Example Question #71 : Integrating
Use a change of variable (aka a u-substitution) to evaluate the integral,
Integrals such as this are seen very commonly in introductory calculus courses. It is often useful to look for patterns such as the fact that the polynomial under the radical in our example, 


Now differentiate with respect to 


Looking at equation (2), we can solve for 


Now proceed with the integration with respect to 

Now write the result in terms of 
Example Question #1 : Use Substitution And Integration
Use u-substitution to fine
Let
Then
Now we can substitute
Now we substitute back
Example Question #73 : Integrating
Evaluate
We can use substitution for this integral.
Let 
then 
Multiplying this last equation by 

Now we can make our substitutions













Example Question #74 : Integrating
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable u to substitute for a variable of x.
For this problem, we will let u replace the expression 
Next, we must take the derivative of u. Its derivative is 
Next, solve this equation for dx so that we may replace it in the integral.
Plug 



The 




The specific steps are as follows:
1.
2.
3.
4.
5.
6.
7.
8.
9.
Example Question #75 : Integrating
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable 














1.
2. 
3.
4.
5.
6.
7.
8.
Example Question #76 : Integrating
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable 














1.
2.
3.
4.
5.
6.
7.
Example Question #77 : Integrating
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable 















1.
2.
3.
4.
5.
6.
7.
Example Question #78 : Integrating
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable 















1.
2.
3.
4.
5.
6.
7.
Example Question #79 : Integrating
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable 













1.
2.
3.
4.
5.
6.
7.
Example Question #521 : Calculus Ab
Solve the following integral using substitution:
To solve the integral, we have to simplify it by using a variable 













1.
2.
3.
4.
5.
6.
7.
8.
Certified Tutor
Certified Tutor
All Calculus AB Resources





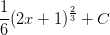
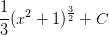


![= \frac{1}{2}\left[\frac{1}{\frac{1}{2}+1}u^{\frac{1}{2}+1} \right ]+C](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741662/gif.latex)





































![\sqrt[3]{(x^3+1)}(\frac{1}{x^2})+c](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/745203/gif.latex)

















































































