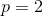All Calculus 2 Resources
Example Questions
Example Question #4 : Comparing Series
Using the Limit Test, determine the nature of the series:
The series is divergent.
The series is convergent.
The series is convergent.
We will use the Limit Comparison Test to study the nature of the series.
We note first that 
We will compare the general term to 
We note that by letting 


Therefore the two series have the same nature, (they either converge or diverge at the same time).
We will use the Integral Test to deduce that the series having the general term:

Note that we know that 
This shows that the series having general term 
By the Limit Test, the series having general term 
This shows that our series is convergent.
Example Question #4 : Comparing Series
Determine the nature of the series having general term:
where
The series is convergent.
The series is divergent.
The series is divergent.
We will use the Comparison Test to prove this result.
We need to note first that 

We know that 

Inverting the above inequality, we have:

Now we will use the Comparison Test.
We know that the series 
Therefore,
is also divergent.
Example Question #11 : Comparing Series
We consider the following series:
Determine the nature of the convergence of the series.
The series is divergent.
The series is divergent.
We will use the Comparison Test to prove this result. We must note the following:

We have all natural numbers n:


Inverting we get :
Summing from 1 to 
We know that the 

Example Question #11 : Comparing Series
Is the series
convergent or divergent, and why?
Divergent, by the comparison test.
Divergent, by the test for divergence.
Convergent, by the ratio test.
Convergent, by the comparison test.
Divergent, by the ratio test.
Convergent, by the comparison test.
We will use the comparison test to prove that
converges (Note: we cannot use the ratio test, because then the ratio will be 
We will compare 


The series
converges, so we must show that

for 
This is easy to show because
since the denominator 


Thus, since
and because
converges, it follows that
converges, by comparison test.
Example Question #12 : Comparing Series
Determine if the series converges or diverges. You do not need to find the sum.
Diverges
Conditionally converges.
Converges
There is not enough information to decide convergence.
Neither converges nor diverges.
Converges
We can compare this to the series 
To figure this out, let's first compare 



There is a rule in math that if you take the reciprocal of each term in an inequality, you are allowed to flip the signs.
Thus, 

And so, because 
Example Question #13 : Comparing Series
For which values of p is

convergent?
it doesn't converge for any values of
only
All positive values of
only
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
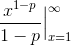
We know that this only goes to zero if 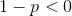

Example Question #13 : Comparing Series
Determine the convergence of the series using the Comparison Test.
Series converges
Series diverges
Cannot be determined
Series converges
We compare this series to the series
Because


it follows that


This implies
Because the series on the right has an exponent 
the series on the right converges
making

converge as well.
Example Question #2951 : Calculus Ii
Determine the convergence of the series using the Comparison Test.
Cannot be determined
Series converges
Series diverges
Series diverges
We compare this series to the series
Because


it follows that


This implies
Because the series on the right has a degree of 

the series on the right diverges
making

diverge as well.
Example Question #2952 : Calculus Ii
Does the series 
Converges to
Converges to
Converges to 1
Diverges
Converges to
Converges to 1
To show this series converges, we use direct comparison with

which converges by the p-series test with 
Thus we must show that

Cross multiplying the previous section and multiplying 


Since this holds for all 

Summing from 




Therefore the series
converges by direct comparison.
Now to find the value, we note that

so that

Now let
be a sequence of partial sums.
Then we have
Therefore

Taking the limit as 
Therefore we have

Example Question #161 : Series In Calculus
Does the series converge?
No
Cannot be determined
Yes
No
Notice that 
This implies that

Which then implies
Since the right-hand side is the harmonic series, we have
and thus the series does NOT converge.
Certified Tutor
Certified Tutor
All Calculus 2 Resources