First we simplify the function using properties of logarithmic functions:

   and 

Therefore:

also

Therefore    

and

to derive this equation we use the product rule:

and

Therefore:

Logarithmic differentiation exploits the properties of logarithms to easily compute derivatives for functions that would otherwise be extremely tedious to find. Direct differentiation using the quotient rule could become quite messy. Take the natural logarithm of both sides of the equation, 

                               (1)

Expand the right-side using the properties of logarithms:

____________________________________________________________

Properties of Logarithmic Functions:

1. 

2. 

3. 

Then proceed with the differentiation using the known derivative of the natural logarithm function and the chain rule: 

____________________________________________________________

Derivative of the Natural Logarithm 

For a function  of , apply the chain-rule, 

____________________________________________________________

Expanding the right-side of equation (1) first by using Property 2. 

Expand the second term with Property 1. Use Property 3 to pull out the exponent in the third term obtained after applying Property 1. 

Differentiating implicitly over both sides of the equation with respect to . Be sure to apply the chain rule as needed. 

So now the derivative we were looking for,  can be solved by multiplying both sides by  and then substituting back in the original function to write everything in terms of 

The farmer's fencing material needs to cover the perimeter of his property. Since this piece of property is shaped like a rectangle, we know that the perimeter can be modeled with the equation

.

In this case, we know that , since the  ft. of fencing need to fit around the whole property.

This problem wants to maximize the area, so we're trying to find which values maximize this equation:

.

We know that 

, or simplified, that .

Solving for  gives us 

,

which we can plug into our area equation, giving us

.

Taking the first derivative gives us 

.

Making  equal zero allows us to solve for . 

.

So,  is 175 ft. To determine if this value is a maximum length, or a minimum, we take the second derivative of our area equation, which yields a constant. Because this value is always less than zero, 175 ft. is a maximum. using our perimeter formula, we see that  is also equal to 175 ft. So, the maximum area the farmer can fence off is 175 ft. x 175 ft., or 30,625  sq. ft.

on this problem we apply the product rule:

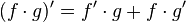
let:       and    

to find the derivative of this function we need to use the chain rule:

let

   and        

and 

and

We start at x = 0 and move to x=2, with a step size of 1. Essentially, we approximate the next step by using the formula:

.

So applying Euler's method, we evaluate using derivative: 

And two step sizes, at x = 1 and x = 2.

And thus the evaluation of p at x = 2, using Euler's method, gives us p(2) = 2.

Using Euler's method with  means that we use two iterations to get the approximation. The general iterative formula is 

where each  is

  is an approximation of , and , for this differential equation. So we have

So our approximation of  is

Euler's method uses iterative equations to find a numerical solution to a differential equation.  The following equations

are solved starting at the initial condition and ending at the desired value.   is the solution to the differential equation.

In this problem,

Starting at the initial point 

We continue using Euler's method until .  The results of Euler's method are in the table below.

Note: Solving this differential equation analytically gives a different answer, .  Future problems will explain this discrepancy. 

Euler's method uses iterative equations to find a numerical solution to a differential equation.  The following equations

are solved starting at the initial condition and ending at the desired value.   is the solution to the differential equation.

In this problem,

Starting at the initial point 

We continue using Euler's method until .  The results of Euler's method are in the table below.

Note: Solving this differential equation analytically gives a different answer, . As the step size gets larger, Euler's method gives a more accurate answer.