We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 2 : Derivative Review

Study concepts, example questions & explanations for Calculus 2

Create An Account

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #461 : Derivative Review

Consider the equation

2x^2 + y^2 = 8xy

where is a function of .

Which of the following is equal to $\frac{\mathrm{d} y}{\mathrm{d} x}$ ?

Possible Answers:

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{2x}{x- 2 y}$

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{x- 2 y}{2x}$

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{2x- 4 y}{4x- y}$

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{4x- 2 y}{4x- y}$

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{4x- y}{2x- 4 y}$

Correct answer:

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{2x- 4 y}{4x- y}$

Explanation:

2x^2 + y^2 = 8xy

$\frac{\mathrm{d} (2x^2 + y^2) }{\mathrm{d} x}=\frac{\mathrm{d} \left (8xy) \right }{\mathrm{d} x}$

$2\; \frac{\mathrm{d} }{\mathrm{d} x} x^2+ \frac{\mathrm{d} }{\mathrm{d} x}y^2=8\: \frac{\mathrm{d} \left \right }{\mathrm{d} x}xy$

$2 \cdot 2x+ 2y \cdot \frac{\mathrm{d}y }{\mathrm{d} x} =8 \left ( y + x \cdot \frac{\mathrm{d} y}{\mathrm{d} x}\right )$

$4x+ 2y \cdot \frac{\mathrm{d}y }{\mathrm{d} x} = 8 y + 8x \cdot \frac{\mathrm{d} y}{\mathrm{d} x}$

$4x- 8 y = 8x \cdot \frac{\mathrm{d} y}{\mathrm{d} x} - 2y \cdot \frac{\mathrm{d}y }{\mathrm{d} x}$

$\left ( 8x- 2y \right )\cdot \frac{\mathrm{d}y }{\mathrm{d} x} = 4x- 8 y$

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{4x- 8 y}{8x- 2y}$

$\frac{\mathrm{d}y }{\mathrm{d} x} = \frac{2x- 4 y}{4x- y}$

Report an Error

Example Question #461 : Derivative Review

Use implicit differentiation to find $\frac{dy}{dx}$ :

$x^4\sin(x+y)=2$

Possible Answers:

$\frac{dy}{dx} = -\left(4\tan(x+y) +1 \right )$

$\frac{dy}{dx} = \frac{4\tan(x+y)}{x}$

$\frac{dy}{dx} = -\left(\frac{4\sin(x+y)-2x}{x\cos x}\right)$

$\frac{dy}{dx} = 2-4x^3\sin (x+y)$

$\frac{dy}{dx}=-\left(\frac{4\tan(x+y)+x}{x} \right )$

Correct answer:

$\frac{dy}{dx}=-\left(\frac{4\tan(x+y)+x}{x} \right )$

Explanation:

To differentiate the left-hand side of the equation, we must use the product rule: f'(x)g(x) +f(x)g'(x) .

Let f(x)=x^4 so that f'(x)=4x^3 , and $g(x)=\sin(x+y)$ so that ${g'(x)=\cos(x+y) \cdot \left(1+\frac{dy}{dx} \right )}$ . After differentiation, we end up with ${4x^3\sin(x+y) +x^4\cos(x+y)\left(1+\frac{dy}{dx} \right )=0}$ .

Using algebra to isolate the $\frac{dy}{dx}$ term, we find that ${\frac{dy}{dx}= -\frac{4x^3 \sin(x+y)}{x^4\cos(x+y)}-1} =-\left(\frac{4\tan(x+y) +x}{x} \right )$ .

Report an Error

Example Question #462 : Derivative Review

Find $\frac{dy}{dx}$ :

$y=x^{\sin x}$

Possible Answers:

$\frac{dy}{dx}= \ln\left( x^{\sin x}\right ) \cos x$

$\frac{dy}{dx} = x^{\sin x}\left(\cos x \ln x + \frac{\sin x}{x} \right )$

$\frac{dy}{dx} = -\cos x \left( x^{\sin x}\right)$

$\frac{dy}{dx} = \cos x \ln x +\frac{\sin x }{x} \right$

$\frac{dy}{dx} = \sin x\left(x^{\cos x} \right )$

Correct answer:

$\frac{dy}{dx} = x^{\sin x}\left(\cos x \ln x + \frac{\sin x}{x} \right )$

Explanation:

Since $\tiny{x}$ is a part of both the base and the exponent, we need to use logarithmic differentiation; that is, take the log of both sides of the equation: $\ln y = \ln (x^{\sin x}) \rightarrow \ln y =\sin x \ln x.$

Differentiating the latter equation, we obtain $\frac{1}{y}\frac{dy}{dx} = \cos x \cdot \ln x +\sin x \cdot \left(\frac{1}{x}\right)$ .

Thus, $\frac{dy}{dx} = x^{\sin x}\left(\cos x \ln x + \frac{\sin x}{x} \right )$ .

Report an Error

Example Question #462 : Derivative Review

Define 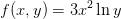$f (x,y) = 3x^{2} \ln y$ .

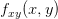
Find $f _{xy} (x,y)$ .

Possible Answers:

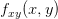
$f _{xy} (x,y) = 6xy$

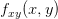
$f _{xy} (x,y) = \frac{6}{xy}$

$f _{xy} (x,y) = \frac{6x }{y}$

$f _{xy} (x,y) = \frac{6y }{x}$

$f _{xy} (x,y) = \frac{6}{xy^{2}}$

Correct answer:

$f _{xy} (x,y) = \frac{6x }{y}$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = 3x^{2} \ln y$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x} 3x^{2} \ln y$

$= 3 \ln y \cdot \frac{\partial }{\partial x} x^{2}$

$= 3 \ln y \cdot 2x$

$= 6x \ln y$

Therefore, $f_{x} (x,y ) = 6x \ln y$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y ) = 6x \ln y$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y} 6x \ln y$

$= 6x \cdot \frac{\partial }{\partial y} \ln y$

$= 6x \cdot \frac{1}{y} = \frac{6x }{y}$

Report an Error

Example Question #463 : Derivative Review

Define $f (x,y) = \tan xy$ .

Find $f _{xy} (x,y)$ .

Possible Answers:

$f_{x} (x,y ) = \sec ^{2} xy + 2 x y \sec ^{2} xy \tan xy$

$f_{x} (x,y ) = \sec xy \tanxy + 2 x y \sec ^{2}xy$

$f_{x} (x,y ) = \sec ^{2} xy + 2 x y \sec ^{3} xy$

$f_{x} (x,y ) = 2 x y \sec ^{2} xy \tan xy$

$f_{x} (x,y ) = \sec xy \tan xy + 2 x y \sec ^{2} xy \tan xy$

Correct answer:

$f_{x} (x,y ) = \sec ^{2} xy + 2 x y \sec ^{2} xy \tan xy$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = \tan xy$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x} \tan xy$

$= \frac{\partial }{\partial x} xy \cdot \sec ^{2} xy$

$= y \sec ^{2} xy$

Therefore, $f_{x} (x,y ) = y \sec ^{2} xy$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y ) = y \sec ^{2} xy$

$f_{x} (x,y ) = \frac{\partial y}{\partial y} \cdot \sec ^{2} xy + y \cdot \frac{\partial }{\partial y} \sec ^{2}xy$

$f_{x} (x,y ) = 1 \cdot \sec ^{2} xy + y \cdot 2 \cdot \frac{\partial }{\partial y}\sec xy \cdot \sec xy$

$f_{x} (x,y ) = \sec ^{2} xy + 2 y \cdot \frac{\partial }{\partial y} xy \cdot \sec xy \tan xy \cdot \sec xy$

$f_{x} (x,y ) = \sec ^{2} xy + 2 y \cdot x \cdot \sec xy \tan xy \cdot \sec xy$

$f_{x} (x,y ) = \sec ^{2} xy + 2 x y \sec ^{2} xy \tan xy$

Report an Error

Example Question #464 : Derivative Review

Define $f (x,y) = e ^{x^{2}+ y^{2}}$ .

Find $f _{xy} (x,y)$ .

Possible Answers:

$f _{xy} (x,y)=2xe ^{x^{2}+y^{2}} + 2y e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)= xy e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)= 4xy e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)=2 xy e ^{x^{2}+y^{2}}$

$f _{xy} (x,y)= xe ^{x^{2}+y^{2}} + y e ^{x^{2}+y^{2}}$

Correct answer:

$f _{xy} (x,y)= 4xy e ^{x^{2}+y^{2}}$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = e ^{x^{2}+ y^{2}} = e ^{x^{2} } e ^{y^{2} }$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x} \left (e ^{x^{2} } e ^{y^{2} } \right )$

$= e ^{y^{2}} \cdot \frac{\partial }{\partial x} \left (e ^{x^{2} }} \right )$

$= e ^{y^{2}} \cdot \frac{\partial }{\partial x} x^{2} \cdot \left (e ^{x^{2} }} \right )$

$= 2x \cdot e ^{y^{2}} \cdot \left (e ^{x^{2} }} \right )$

$= 2x e ^{x^{2}} e ^{y^{2}}$

Therefore, $f_{x} (x,y ) = 2x e ^{x^{2}} e ^{y^{2}}$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y )= 2x e ^{x^{2}} e ^{y^{2}}$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y} \left ( 2x e ^{x^{2}} e ^{y^{2}} \right )$

$=2x e ^{x^{2}} \frac{\partial }{\partial y} \left ( e ^{y^{2}} \right )$

$=2x e ^{x^{2}} \frac{\partial }{\partial y} \left ( y^{2} \right ) e ^{y^{2}}$

$=2x e ^{x^{2}} \cdot 2y \cdot e ^{y^{2}}$

$=4xy e ^{x^{2}} e ^{y^{2}} = 4xy e ^{x^{2}+y^{2}}$

Report an Error

Example Question #464 : Derivative Review

Define $f (x,y) = \cos (x^{2} + y^{2})$ .

Find $f _{xy} (x,y)$ .

Possible Answers:

$f _{xy} (x,y) = 4xy \cos (x^{2} + y^{2})$

$f _{xy} (x,y) = 4x \cos (x^{2} + y^{2}) - 4y \cos (x^{2} + y^{2})$

$f _{xy} (x,y) = 4x \cos (x^{2} + y^{2}) + 4y \cos (x^{2} + y^{2})$

$f _{xy} (x,y) =- 4xy \cos (x^{2} + y^{2})$

$f _{xy} (x,y) =- 4x \cos (x^{2} + y^{2}) + 4y \cos (x^{2} + y^{2})$

Correct answer:

$f _{xy} (x,y) =- 4xy \cos (x^{2} + y^{2})$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = \cos (x^{2} + y^{2})$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x} \cos (x^{2} + y^{2})$

$= \frac{\partial }{\partial x}(x^{2} + y^{2}) \cdot \left [ - \sin (x^{2} + y^{2}) \right ]$

$= (2x + 0) \cdot \left [ - \sin (x^{2} + y^{2}) \right ]$

$= - 2x\sin (x^{2} + y^{2})$

Therefore, $f_{x} (x,y ) = - 2x\sin (x^{2} + y^{2})$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y ) = - 2x\sin (x^{2} + y^{2})$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y}\left [ - 2x\sin (x^{2} + y^{2}) \right ]$

$=- 2x \frac{\partial }{\partial y}\left [ \sin (x^{2} + y^{2}) \right ]$

$=- 2x\cdot \frac{\partial }{\partial y}(x^{2} + y^{2}) \cdot \cos (x^{2} + y^{2})$

$=- 2x\cdot (0 + 2y) \cdot \cos (x^{2} + y^{2})$

$=- 2x\cdot ( 2y) \cdot \cos (x^{2} + y^{2})$

$=- 4xy \cos (x^{2} + y^{2})$

Report an Error

Example Question #1591 : Calculus Ii

Define $f (x,y) = \log xy$ .

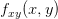
Find $f _{xy} (x,y)$ .

Possible Answers:

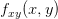
$f _{xy} (x,y) = 0$

$f _{xy} (x,y) = \frac{1}{x+y}$

$f _{xy} (x,y) = 1$

$f _{xy} (x,y) = \frac{1}{xy}$

$f _{xy} (x,y) = \frac{x+y}{x y}$

Correct answer:

$f _{xy} (x,y) = 0$

Explanation:

First, find $f_{x} = \frac{\partial f}{\partial x}$ as follows:

$f (x,y) = \log xy = \log x + \log y = \frac{ \ln x }{\ln 10}+ \frac{ \ln y }{\ln 10}$

$f (x,y) = \frac{ 1}{\ln 10}\left ( \ln x+ \ln y \right )$

$\frac{\partial }{\partial x}f (x,y) = \frac{\partial }{\partial x}\left [ \frac{ 1}{\ln 10}\left ( \ln x+ \ln y \right ) \right ]$

$= \frac{ 1}{\ln 10} \left (\frac{\partial }{\partial x}\left \ln x+\frac{\partial }{\partial x} \ln y \right )$

$= \frac{ 1}{\ln 10} \left ( \frac{1}{x}+0 \right )$

$= \frac{ 1}{\ln 10} \cdot \frac{1}{x}$

Therefore, $f_{x} (x,y )= \frac{ 1}{\ln 10} \cdot \frac{1}{x}$ .

Now, find $f_{xy} = \frac{\partial }{\partial y} f_{x}$ as follows:

$f_{x} (x,y )= \frac{ 1}{\ln 10} \cdot \frac{1}{x}$

$\frac{\partial }{\partial y} f_{x} (x,y ) = \frac{\partial }{\partial y}\left ( \frac{ 1}{\ln 10} \cdot \frac{1}{x} \right )$

Report an Error

Example Question #1592 : Calculus Ii

Let the initial approximation of a solution of the equation

$e^{x} = \sin x$

be $x_{1} = -2$ .

Use one iteration of Newton's method to find an approximation for $x_{2}$ . Give your answer to the nearest thousandth.

Possible Answers:

-3.895

-4.195

-3.695

-3.795

-4.095

Correct answer:

-3.895

Explanation:

Rewrite the equation to be solved for as $e^{x} - \sin x = 0$ .

Let $f(x ) = e^{x} - \sin x$ .

$f'(x ) = \frac{\mathrm{d} }{\mathrm{d} x} \left (e^{x} - \sin x \right )$

$f'(x ) = e^{x} - \cos x \right )$

The problem amounts to finding a zero of f(x ) . By Newton's method, the second approximation can be derived from the first using the equation

$x_{2} = x_{1} - \frac{f(x_{1})}{f'(x_{1})}$ .

Since $x_{1} = -2$ ,

$f(-2 ) = e^{-2} - \sin (-2) \approx 0.1353 - (-0.9093 ) \approx 1.0446$

and

$f'(-2 ) = e^{-2} - \cos (-2) \approx 0.1353 - \left ( -0.4161 \right )\approx 0.5514$

Use these to find the approximation:

$x_{2} =-2 - \frac{f(-2)}{f'(-2)} \approx -2 - \frac{1.0446}{0.5514}\approx -2 -1.8945 \approx -3.895$

Report an Error

Example Question #467 : Derivative Review

Define f(x) = e^x- 4x .

Give the minimum value of on the set of all real numbers.

Possible Answers:

$4 - 4 \ln 4$

$2- 4 \ln 2$

The function has no miminum value.

e^4 - 16

e^2 - 4

Correct answer:

$4 - 4 \ln 4$

Explanation:

This function is continuous and differentiable everywhere. First we find the value(s) of for which f'(x) =0 .

f(x) = e^x- 4x

$f'(x) =\frac{\mathrm{d} }{\mathrm{d} x}\left ( e^x- 4x \right )$

f'(x) = e^x- 4

f'(x) =0

e^x- 4 =0

e^x= 4

$\ln e^x= \ln 4$

$x= \ln 4$

Therefore, this is the only possible minimum. We determine whether it is a minimum by evaluating $f''(\ln 4)$ :

f'(x) = e^x- 4

$f''(x) = \frac{\mathrm{d} }{\mathrm{d} x} \left ( e^x- 4 \right )$

f''(x) = e^x

$f''(\ln 4) = e^{\ln 4} = 4 > 0$

Since $f''(\ln 4) > 0$ , has its minimum value at $x= \ln 4$ ; it is

$f( \ln 4) = e^{ \ln 4}- 4 \cdot \ln 4 = 4 - 4 \ln 4$ .

Report an Error

View Calculus 2 Tutors

Nicole
Certified Tutor

College of St Benedict, Bachelor in Arts, Economics. University of South Florida-Main Campus, Master of Arts, Economics.

View Calculus 2 Tutors

Hirdeshwar
Certified Tutor

Indian Institute of Technology, Powai, Bombay, India, Doctor of Philosophy, Mathematics.

View Calculus 2 Tutors

MEER
Certified Tutor

IIT , Master's/Graduate, Microelectronics .

All Calculus 2 Resources

9 Diagnostic Tests 308 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Algebra Tutors in Phoenix, Biology Tutors in Philadelphia, Calculus Tutors in Seattle, Statistics Tutors in Chicago, SAT Tutors in Houston, Reading Tutors in New York City, GRE Tutors in Washington DC, SSAT Tutors in Los Angeles, Algebra Tutors in Miami, ISEE Tutors in Atlanta

Popular Courses & Classes

SSAT Courses & Classes in Chicago, GMAT Courses & Classes in San Diego, SSAT Courses & Classes in San Diego, SAT Courses & Classes in Philadelphia, SSAT Courses & Classes in New York City, GMAT Courses & Classes in Seattle, SSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Los Angeles, SSAT Courses & Classes in Washington DC, MCAT Courses & Classes in Los Angeles

Popular Test Prep

MCAT Test Prep in Denver, SSAT Test Prep in Philadelphia, ISEE Test Prep in Seattle, SSAT Test Prep in Atlanta, SSAT Test Prep in Houston, LSAT Test Prep in Houston, GRE Test Prep in Chicago, SAT Test Prep in Dallas Fort Worth, GMAT Test Prep in New York City, LSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 2 : Derivative Review

Study concepts, example questions & explanations for Calculus 2

All Calculus 2 Resources

Example Questions

Example Question #461 : Derivative Review

Example Question #461 : Derivative Review

Example Question #462 : Derivative Review

Example Question #462 : Derivative Review

Example Question #463 : Derivative Review

Example Question #464 : Derivative Review

Example Question #464 : Derivative Review

Example Question #1591 : Calculus Ii

Example Question #1592 : Calculus Ii

Example Question #467 : Derivative Review

All Calculus 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: