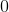All Calculus 2 Resources
Example Questions
Example Question #1 : Derivatives
Evaluate the limit using one of the definitions of a derivative.
Does not exist
Evaluating the limit directly will produce an indeterminant solution of 
The limit definition of a derivative is 

Let 


Thus, the limit is
Example Question #2 : Derivatives
Evaluate the limit using one of the definitions of a derivative.
Does not exist
Evaluating the derivative directly will produce an indeterminant solution of 
The limit definition of a derivative is 

Let 



Example Question #3 : Derivatives
Suppose 



None of the other answers
None of the other answers
The correct answer is 11.
Taking the derivative of 
Substituting 

Example Question #4 : Definition Of Derivative
Evaluate the limit
without using L'Hopital's rule.
If we recall the definition of a derivative of a function 


If we compare this definition to the limit
we see that that this is the limit definition of a derivative, so we need to find the function 




We know that the derivative is 

Example Question #1 : Derivatives
Approximate the derivative if 

Write the definition of the limit.
Substitute 
Since 


The best answer is:
Example Question #2 : Derivatives
Given:
Find f'(x):
Computation of the derivative requires the use of the Product Rule and Chain Rule.
The Product Rule is used in a scenario when one has two differentiable functions multiplied by each other:
This can be easily stated in words as: "First times the derivative of the second, plus the second times the derivative of the first."
In the problem statement, we are given:


The "Second" function requires use of the Chain Rule.
When:
Applying these formulas results in:
Simplifying the terms inside the brackets results in:
We notice that there is a common term that can be factored out in the sets of equations on either side of the "+" sign. Let's factor these out, and make the equation look "cleaner".
Inside the brackets, it is possible to clean up the terms into one expanded function. Let us do this:
Simplifying this results in one of the answer choices:
Example Question #4 : Derivatives
What is the value of the limit below?
Recall that one definition for the derivative of a function 

This means that this question is asking us to find the value of the derivative of 

Since



Example Question #2 : Derivative Rules For Sums, Products, And Quotients
Evaluation of this integral requires use of the Product Rule. One must also need to recall the form of the derivative of 
Product Rule:
Applying these two rules results in:
This matches one of the answer choices.
Example Question #3 : Derivative Review
Use the definition of the derivative to solve for 
In order to find 

Definition of Derivative:
Now lets apply this to our problem.
Now lets expand the numerator.
We can simplify this to
Now factor out an h to get
We can simplify and then evaluate the limit.
Example Question #5 : Derivatives
Use the definition of the derivative to solve for 
In order to find 

Definition of Derivative:
Now lets apply this to our problem.
Now lets expand the numerator.
We can simplify this to
Now factor out an h to get
We can simplify and then evaluate the limit.
All Calculus 2 Resources

















![h'(x)=[f(x+2)][-g'(-x)]+[g(-x)][f'(x+2)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/250996/gif.latex)

























![\frac{d}{dx}[f(x)*g(x)]=f(x)*g'(x)+g(x)*f(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/400721/gif.latex)


![f'(x)=(3x^2)[5(x^2-5x+2)^4(2x-5)]+(x^2-5x+2)^5(6x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/400726/gif.latex)
![f'(x)=(3x^2)[(10x-25)(x^2-5x+2)^4]+(x^2-5x+2)^5(6x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/400727/gif.latex)
![f'(x)=(x^2-5x+2)^4[(3x^2)(10x-25)+(6x)(x^2-5x+2)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/400728/gif.latex)
![f'(x)=(x^2-5x+2)^4[30x^3-75x^2+6x^3-30x^2+12x]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/400729/gif.latex)













![\frac{d}{dx}[f(x)g(x)]=f(x)g'(x)+g(x)f'(x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/430297/gif.latex)
![\frac{d}{dx}[\tan^{-1}(u)]=\frac{1}{1+u^2}\frac{du}{dx}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/430298/gif.latex)
![\frac{dy}{dx}=\frac{d}{dx}[x^2\tan^{-1}(3x^5)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/430299/gif.latex)