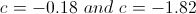Call Now to Set Up Tutoring:

(888) 888-0446

Calculus 1 : Points

Study concepts, example questions & explanations for Calculus 1

Create An Account

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #11 : Points Of Inflection

Where does the function $f(x)=5x^{3}+\frac{5}{3}x^2+11$ have a point of inflection?

Possible Answers:

$x=-\frac{1}{9}$

$x=-\frac{1}{6}$

$x=-\frac{1}{3}$

$x=\frac{1}{9}$

$x=\frac{1}{3}$

Correct answer:

$x=-\frac{1}{9}$

Explanation:

The point of inflection of an object can be found by setting the second derivative of the function equal to zero and solving.

$f'(x)=15x^2+\frac{10}{3}x.$

$f''(x)=30x+\frac{10}{3}=0.$

$30x=-\frac{10}{3}, x=-\frac{1}{9}.$

Report an Error

Example Question #2573 : Calculus

Find the value of the point of inflection of the function $f(x)=\frac{12x-\frac{8}{3}x^5}{x^2}$ .

Possible Answers:

$x=(\frac{3}{2})^{4}$

$x=(\frac{3}{2})^2$

$x=(\frac{2}{3})^{2}$

$x=(\frac{2}{3})^{\frac{1}{4}}$

$x=(\frac{3}{2})^{\frac{1}{4}}$

Correct answer:

$x=(\frac{3}{2})^{\frac{1}{4}}$

Explanation:

First, we need to simplify the expression. Sine the numerator has more terms than the denominator, we can simply divide out both terms.

$\frac{12x-\frac{8}{3}x^5}{x^2}=12x^{-1}-\frac{8}{3}x^3$ .

Now, we must compute the second derivative of this function, and set it equal to zero.

$f'(x)=-12x^{-2}-8x^2$ .

$f''(x)=24x^{-3}-16x=0.$

$x^{-4}=\frac{2}{3}$ .

$x=(\frac{3}{2})^{\frac{1}{4}}$ .

Report an Error

Example Question #2574 : Calculus

Find the points of inflection for the following function:

f(x)=x^3+5x^2+5x

Possible Answers:

$(-\frac{5}{3}, \frac{25}{27})$

$(-\frac{5}{3}, -\frac{25}{27})$

(0, 0)

$(-\frac{5}{3}, 0)$

Correct answer:

$(-\frac{5}{3}, \frac{25}{27})$

Explanation:

To find the points of inflection, we must find the points at which the second derivative of the function changes sign.

First, we must find the second derivative:

f'(x)=3x^2+10x+5

f''(x)=6x+10

The derivatives were found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Next, we must find the x value at which the second derivative is equal to zero:

$x=-\frac{5}{3}$

Using this value, we make our intervals on which we examine the sign of the second derivative:

$(-\infty, -\frac{5}{3}), (-\frac{5}{3}, \infty)$

Note that at the endpoints of the intervals, the second derivative is neither positive nor negative.

Now, simply plug in any value on the interval into the second derivative function and check the sign. On the first interval, the second derivative is negative, while on the second interval, it is positive. Thus, a point of inflection exists at $x=-\frac{5}{3}$ . To get the y-coordinate, simply evaluate the function at this x value:

$f(-\frac{5}{3})=\frac{25}{27}$

The point of inflection is $(-\frac{5}{3}, \frac{25}{27})$ .

Report an Error

Example Question #21 : Points Of Inflection

Determine the points of inflection for the following function:

$f(x)=\frac{x^3}{3}+x^2+x+1$

Possible Answers:

x=2

x=0

x=1

x=-1

Correct answer:

x=-1

Explanation:

To determine the points of inflection, we must determine the x values at which the second derivative changes in sign.

So, we must first find the second derivative:

f'(x)=x^2+2x+1

f''(x)=2x+2

The derivatives were found using the rule

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Next, we must find the values at which the second derivative is equal to zero:

2(x+1)=0

x=-1

Now, using this zero, we can make the intervals on which we check the sign of the second derivative:

$(-\infty, -1), (-1, \infty)$

Note that at the endpoints, the second derivative is neither positive nor negative.

Plug in any value on each interval into the second derivative function and check the sign. On the first interval, the second derivative is negative, while on the second, it is positive. Because a sign change occured at x=-1 , there exists the point of inflection.

Report an Error

Example Question #2576 : Calculus

Determine the points of inflection for the following function:

f(x)=x^3+10x^2+x

Possible Answers:

$x=\frac{-20+\sqrt{388}}{6}$

$x=-\frac{20}{3}$

$x=-\frac{10}{3}$

$x=\frac{10}{3}$

Correct answer:

$x=-\frac{10}{3}$

Explanation:

To determine the points of inflection of the function, we must determine where the second derivative of the function changes sign.

First, we find the second derivative:

f'(x)=3x^2+20x+1

f''(x)=6x+20

The derivatives were found using the following rule:

$\frac{\mathrm{d} }{\mathrm{d} x} x^n=nx^{n-1}$

Now, we must find where the second derivative equals zero:

2(3x+10)=0

$x=-\frac{10}{3}$

Using this value, we can now create the intervals on which we check the sign of the second derivative:

$(-\infty, -\frac{10}{3}), (-\frac{10}{3}, \infty)$

Note that at the endpoints of the intervals, the second derivative is neither positive nor negative.

To check the second derivative's sign on each interval, simply plug in any point on the interval into the second derivative function. On the first interval, the second derivative is negative, while on the second interval, it is positive. Because the sign of the second derivative changes at $x=-\frac{10}{3}$ , there exists the point of inflection.

Report an Error

Example Question #1 : Second Derivatives

What are the coordinates of the points of inflection for the graph

$y=\frac{x^4}{12}+x^3+4x^2-8x+5?$

Possible Answers:

x=-4,-2

x=4,-2

There are no points of inflection on this graph.

x=4,2

x=-4,2

Correct answer:

x=-4,-2

Explanation:

Infelction points are the points of a graph where the concavity of the graph changes. The inflection points of a graph are found by taking the double derivative of the graph equation, setting it equal to zero, then solving for .

To take the derivative of this equation, we must use the power rule,

$\frac{d}{dx}x^n=nx^{n-1}$ .

We also must remember that the derivative of an constant is 0.

After taking the first derivative of the graph equation using the power rule, the equation becomes

$y^{'}=\frac{x^3}{3}+3x^2+8x-8$ .

In this problem the double derivative of the graph equation comes out to $y^{''}=x^2+6x+8$ , factoring this equation out it becomes $y^{''}=(x+4)(x+2)$ .

Solving for when the equation is set equal to zero, the inflection points are located at x=-4 , -2 .

Report an Error

Example Question #91 : Graphing Functions

Find the critical points (rounded to two decimal places):

f(x)= x^3+3x^2+x

Possible Answers:

$c=0.18\ and\ c=1.82$

$c=0.25\ and\ c=2.41$

$c=-0.25\ and\ c=-2.41$

$c=-0.18\ and\ c=-1.82$

Correct answer:

$c=-0.18\ and\ c=-1.82$

Explanation:

To find the critical points, set f{}'(x)=0 and solve for .

f(x)= x^3+3x^2+x

Differentiate:

$f{}'(x)= 3x^2+6x+1$

Set equal to zero:

3x^2+6x+1=0

Solve for using the quadratic formula: $x= \frac{-b\pm \sqrt{b^2-4ac}}{2a}$

$a=3,\ b=6,\ c=1$

$x= \frac{-6\pm \sqrt{(6)^2-4(3)(1)}}{2(3)}$

$x= \frac{-6\pm \sqrt{36-12}}{6}}$

$x= \frac{-6+\sqrt{24}}{6}}\ and\ x= \frac{-6-\sqrt{24}}{6}}$

$c=-0.18\ and\ c=-1.82$

Report an Error

Example Question #2 : How To Graph Functions Of Points

Find the value(s) of the critical point(s) of

f(x)=x^3+2x^2+x+4 .

Possible Answers:

$\\ c_1=-\frac{1}{3} \\ \\ c_2=-1$

$\\ c_1=3 \\ \\ c_2=-1$

$\\ c_1=-3 \\ \\ c_2=1$

$\\ c_1=\frac{1}{3} \\ \\ c_2=1$

There are no real answers.

Correct answer:

$\\ c_1=-\frac{1}{3} \\ \\ c_2=-1$

Explanation:

In order to find the critical points, we must find $\ f'(x)$ and solve for $\ x$

f(x)=x^3+2x^2+x+4

$\\ \\ f'(x)=3x^2+4x+1$

Set f'(x)=0

$\\ \\ 3x^2+4x+1=0$

Use the quadratic equation to solve for $\ x$ .

Remember that the quadratic equation is as follows.

$\\ \\ x=\frac{-b\pm\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$ , where a,b and c refer to the coefficents in the

equation ax^2+bx+c=0 .

In this case, a=3 , b=4 , and c=1 .

After plugging in those values, we get

$\\ \\ x=\frac{-4\pm\sqrt{4^2-4\cdot3\cdot1}}{2\cdot3} =\frac{-4 \pm \sqrt{4}}{6}=\frac{-4 \pm 2}{6}$ .

So the critical points values are:

$\\ \\ c_1=\frac{-4+2}{6}=\frac{-1}{3}$

$\\ \\ c_2=\frac{-4-2}{6}=-1$

Report an Error

Example Question #3 : How To Graph Functions Of Points

Find the value(s) of the critical point(s) of

f(x)=5x^3+10x^2+x+100 .

Possible Answers:

$\\ c_1=\frac{\sqrt{85}}{15} \\ \\ c_2=\frac{-\sqrt{85}}{15}$

$\\ c_1=0 \\ \\ c_2=0$

$\\ c_1=1 \\ \\ c_2=0$

$\\ c_1=\frac{-10+\sqrt{85}}{30} \\ \\ c_2=\frac{-10-\sqrt{85}}{30}$

$\\ c_1=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-10-\sqrt{85}}{15}$

Correct answer:

$\\ c_1=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-10-\sqrt{85}}{15}$

Explanation:

In order to find the critical points, we must find $\ f'(x)$ and solve for $\ x$ .

$\\ \\ f(x)=5x^3+10x^2+x+100$

$\\ \\ f'(x)=15x^2+20x+1$

Set $\ f'(x)=0$

$\\ \\ 15x^2+20x+1=0$

Use the quadratic equation to solve for $\ x$ .

Remember that the quadratic equation is as follows.

$\\ \\ x=\frac{-b\pm\sqrt{b^2-4\cdot a\cdot c}}{2\cdot a}$ , where a,b and c refer to the coefficents in the equation ax^2+bx+c=0 .

In this case, a=15 , b=20 , and c=1 .

After plugging in those values, we get.

${}\\ x=\frac{-20\pm\sqrt{20^2-4\cdot15\cdot1}}{2\cdot15} =\frac{-20 \pm \sqrt{340}}{30} \\ \\ x=\frac{-20 \pm 2\cdot\sqrt{85}}{30}$

So the critical points values are,

${}\\ \\ c_1=\frac{-20+2\cdot \sqrt{85}}{30}=\frac{-10+\sqrt{85}}{15} \\ \\ c_2=\frac{-20-2\cdot \sqrt{85}}{30}=\frac{-10-\sqrt{85}}{15}$

Report an Error

Example Question #2 : How To Graph Functions Of Points

Find the critical points of

f(x)=x^3+3x^2+x+5

Possible Answers:

$\\ c_1=\frac{\sqrt{6}}{3}\\\\\ c_2=-\frac{\sqrt{6}}{3}$

The critical points are complex.

$\\ c_1=-1+\frac{\sqrt{6}}{3}\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

$\\ c_1=0\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

Correct answer:

$\\ c_1=-1+\frac{\sqrt{6}}{3}\\\\\ c_2=-1-\frac{\sqrt{6}}{3}$

Explanation:

First we need to find f'(x) .

f(x)=x^3+3x^2+x+5

f'(x)=3x^2+6x+1

Now we set f'(x)=0.

3x^2+6x+4=0.

Now we can use the quadratic equation in order to find the critical points.

Remember that the quadratic equation is

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$ ,

where a,b,c refer to the coefficients in the equation

ax^2+bx+c=0

In this case, a=3, b=6, and c=1.

$x=\frac{-6\pm\sqrt{(-6)^2-4(3)(1)}}{(2)(3)}$

$x=\frac{-6\pm\sqrt{24}}{6}=\frac{-6\pm2\sqrt{6}}{6}$

Thus are critical points are

$c_1=\frac{-6+2\sqrt{6}}{6}=-1+\frac{\sqrt{6}}{3}$

$c_2=\frac{-6-2\sqrt{6}}{6}=-1-\frac{\sqrt{6}}{3}$

Report an Error

View Calculus Tutors

James
Certified Tutor

Purdue University-Main Campus, Doctor of Education, Mathematics Teacher Education.

View Calculus Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View Calculus Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All Calculus 1 Resources

10 Diagnostic Tests 438 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in San Diego, Algebra Tutors in Miami, GMAT Tutors in Miami, Biology Tutors in Chicago, Reading Tutors in Houston, SAT Tutors in Phoenix, SAT Tutors in Boston, Reading Tutors in Philadelphia, Spanish Tutors in New York City, Algebra Tutors in Seattle

Popular Courses & Classes

SAT Courses & Classes in Philadelphia, GRE Courses & Classes in Philadelphia, ISEE Courses & Classes in Los Angeles, SSAT Courses & Classes in San Diego, SAT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in Boston, SSAT Courses & Classes in Denver, ACT Courses & Classes in Los Angeles, SSAT Courses & Classes in Atlanta, GMAT Courses & Classes in New York City

Popular Test Prep

GMAT Test Prep in Boston, ISEE Test Prep in Seattle, ISEE Test Prep in Boston, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Atlanta, LSAT Test Prep in New York City, GRE Test Prep in Philadelphia, GMAT Test Prep in Seattle, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Calculus 1 : Points

Study concepts, example questions & explanations for Calculus 1

All Calculus 1 Resources

Example Questions

Example Question #11 : Points Of Inflection

Example Question #2573 : Calculus

Example Question #2574 : Calculus

Example Question #21 : Points Of Inflection

Example Question #2576 : Calculus

Example Question #1 : Second Derivatives

Example Question #91 : Graphing Functions

Example Question #2 : How To Graph Functions Of Points

Example Question #3 : How To Graph Functions Of Points

Example Question #2 : How To Graph Functions Of Points

All Calculus 1 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: