All Calculus 1 Resources
Example Questions
Example Question #8 : How To Find Increasing Intervals By Graphing Functions
Below is the complete graph of 

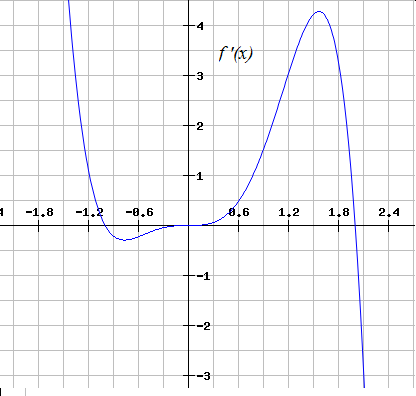




Example Question #9 : How To Find Increasing Intervals By Graphing Functions
Function A
Function B
Function C
Function D
Function E
5 graphs of different functions are shown above. Which graph shows an increasing/non-decreasing function?
Function A
Function E
Function D
Function C
Function B
Function E
A function 


Function E is the only function that has this property. Note that function E is increasing, but not strictly increasing
Example Question #3 : Increasing Intervals
Find the increasing intervals of the following function on the interval 
To find the increasing intervals of a given function, one must determine the intervals where the function has a positive first derivative. To find these intervals, first find the critical values, or the points at which the first derivative of the function is equal to zero.
For the given function, 
This derivative was found by using the power rule

When set equal to zero, 





Example Question #11 : Increasing Intervals
Is 

f(x) is decreasing at the point, because f'(x) is negative.
f(x) is increasing at the point, because f'(x) is positive.
f(x) is decreasing at the point, because f'(x) is positive.
f(x) is flat at the point, because f'(x) is zero.
f(x) is decreasing at the point, because f'(x) is negative.
Is f(x) increasing, decreasing, or flat at 
Recall that to find if a function is increasing or decreasing, we can use its first derivative. If f'(x) is positive, f(x) is increasing. If f'(x) is negative, f(x) is decreasing.
So, given:
We get
Then:
Therefore, f(x) is decreasing at the point, because f'(x) is negative.
Example Question #31 : Intervals
Tell whether 
![[4,7]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/384983/gif.latex)
Decreasing, because g'(t) is negative.
Increasing, because g'(t) is positive.
Decreasing, because g'(t) is positive.
Increasing, because g'(t) is negative.
Increasing, because g'(t) is positive.
Tell whether g(t) is increasing or decreasing on the interval [4,7]
To find increasing and decreasing, find where the first derivative is positive and negative. If g'(t) is positive, then g(t) is increasing and vice-versa.
Then,plug in the endpoints of [4,7] and see what you get for a sign.
So, since g'(t) is positive on the interval, g(t) is increasing.
Example Question #13 : Increasing Intervals
Find the interval on which the function is increasing:
The function is never increasing.
To find the interval(s) on which the function is increasing, we must find the intervals on which the first derivative of the function is positive.
The first derivative of the function is:
and was found using the rule
Now we must find the critical value, at which the first derivative is equal to zero:
Now, we make the intervals on which we look at the sign of the first derivative:
On the first interval the first derivative is positive, while on the second it is negative. Thus, the first interval is our answer, because over this range of x values, the first derivative is positive and the function is increasing.
Example Question #14 : Increasing Intervals
Suppose 







If 





Example Question #15 : Increasing Intervals
Deletable Note to the admin: I am virtually 100% sure the derivative has been correct. Derivative of the top is 6x. Derivative of the bottom is 1/x. So numerator of derivative by quotient rule is 
Let 


Every nontrivial subinterval of
No subinterval of 
Only intervals where 
Every nontrivial subinterval of
Take the first derivative of 






is positive for all positive 


NOTE: Interestingly the opposite of the choice 








Example Question #16 : Increasing Intervals
Find the intervals on which the following function is increasing:
To find the intervals on which the function is increasing, we must find the intervals where the first derivative is positive. To do this, we must find the first derivative, and find its critical values (at which the first derivative is equal to zero):
The derivative was found using the following rule:
Now, write the intervals of the function for which c is the upper and lower bound:
Note that at the critical value, the derivative is neither positive nor negative.
Now, we analyze the sign of the derivative within each interval; on the first interval, the derivative is always negative, but on the second interval, the first derivative is always positive. In other words, for this set of values - 
Example Question #17 : Increasing Intervals
Determint the intervals on which the following function is increasing:
To determine the intervals on which the function is increasing, we must determine the intervals on which the first derivative of the function is positive. To start, we must find the first derivative:
The derivative was found using the following rule:
The first derivative is a positive constant, therefore the function is increasing on the entire domain, 
Certified Tutor
All Calculus 1 Resources


























































