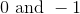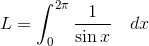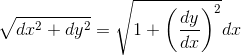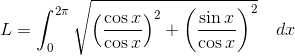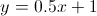All Calculus 1 Resources
Example Questions
Example Question #3 : Relative Extremum
Determine the relative maxima for the function:
To determine the relative maxima for the function, we must determine where the first derivative of the function changes from positive to negative.
The first derivative of the function is
and was found using the following rule:
Next, we must find the critical points, the values at which the first derivative is equal to zero:
Using the critical values, we can then create the intervals on which we evaluate the sign of the first derivative:
To check the sign of the first derivative, plug in any value on each interval into the first derivative function. On the first interval, the first derivative is positive, on the second, it is negative, and on the third it is positive. The first derivative changes from positive to negative at 
Example Question #4 : Relative Extremum
Find the local max of

using the equation and/or the following graph.

We notice that this function has 2 extrema which are located at 


We know that extrema exist when the slope of the function is zero, hence we take the derivative, set it equal to zero, and than solve for x.
The derivative is the following:

Therefore setting both pieces equal to zero we see the following:


Finding out if one of these x values produce a local min or max however requires either the first derivative test, the second derivative test, or analyzing the graph. We see that for a small neighborhood around 




Therefore when 
Example Question #2 : Relative Extremum
The following is a list of values at certain points for continuous 
At least 2
Exactly 2
Exactly 1
At most 2
At least 1
At least 2
The mean value theorem states that if continuous 


Example Question #6 : Relative Extremum
A relative minimum of a function is all the points x, in the domain of the function, such that it is the smallest value for some neighborhood. These are points in which the first derivative is 0 or it does not exist.
Find the relative minimum of the function

using the following graph and the function.

We notice that this function has 2 extrema which are located at x=-1 and x=0. We could have also of found this by looking at the function itself:

We know that extrema exist when the slope of the function is zero, hence we take the derivative, set it equal to zero, and than solve for x.
The derivative is the following:

Therefore setting both pieces equal to zero we see the following:


Finding out if one of these x values produce a local min or max however requires either the first derivative test, the second derivative test, or analyzing the graph. We see that for a small neighborhood around 
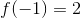



Example Question #1 : Length Of Line
Consider a function 

Which integral can calculate the length along this curve between 

This is not possible with the information given.
To determine the length of a curve between two points, we evaluate the integral
There are many reasons this works, but we'll give an informal explanation here:
If we divide this curve into three line-segments, we can see that they become more and more similar to the original curve. By adding up all the little hypotenuses, we can arrive at the length of the curve. Note, that
If we think of the integration symbol as a sum of infinitely small parts, this gets us the formula for length:

Returning to the problem, we plug the derivative into the length formula:
substitute:
Simplify:
By trigonometric identities we get:
Example Question #2 : How To Find Length Of Line By Graphing Functions
Find the length of the line segment between points A and B:
The distance between two points can be easily found using the Distance Formula:
Applying the points we are given to this formula results in:
This is one of the answer choices.
Example Question #1671 : Functions
What is the equation of the line tangent to f(x) = 4x3 – 2x2 + 4 at x = 5?
y = 44x + 245
y = 85x + 24
y = 280x – 946
None of the other answers
y = 220x – 550
y = 280x – 946
First, take the derivative of f(x). This is very easy:
f'(x) = 12x2 – 4x
Now, the slope of the tangent line at x = 5 is f'(5). Evaluated, this is: f'(5) = 12 * 5 * 5 – 4 * 5 = 300 – 20 = 280
Now, we must find the intersection point on the original line:
f(5) = 4 * 53 – 2 * 52 + 4 = 500 – 50 + 4 = 454
Therefore, the point of tangent intersection is (5,454).
Using the point-slope form of linear equations, we can find the line:
(y – 454) = 280(x – 5)
y – 454 = 280x – 1400
y = 280x – 946
Example Question #2 : Lines
Find the equation of the line tangent to 

The equation of the tangent line will have the form 


To find the slope, we need to evaluate the derivative at 

Now that we have the slope, we can determine the equation of the tangent line using the point-slope formula:
Example Question #3 : Equation Of Line
Find the equation of the line tangent to 

To find the equation of the line at that point, you need two things: the slope at that point and the y adjustment of the function, in the form 





To find the y adjustment pick a point 0 in the original



Now you simply solve for 

Final equation of the line tangent to 

Example Question #1 : Lines
Find the equation of the line tangent to 

To get the slope, find the derivative of 



Remember that the derivative of 
To find the 







The coefficient in front of the 
Now you simply solve for 

Final equation of the line tangent to 


Certified Tutor
Certified Tutor
All Calculus 1 Resources