All Basic Geometry Resources
Example Questions
Example Question #1323 : Plane Geometry
If one leg of a right triangle is 6in and the other leg is 8in, what is the measure of the hypotenuse?
First we need to know Pythagorean Theorem states that what when we take the square of one leg and add it to the square of the other leg, we get the hypotenuse squared or 
Since the short legs of our triangles are 6 and 8 we can set up our equation as follows:

Now we solve

Since 

So the hypotenuse measures 10 inches.
Example Question #51 : How To Find The Length Of The Hypotenuse Of A Right Triangle : Pythagorean Theorem
Susie walks north from her house to a park that is 30 meters away. Once she arrives at the park, she turns and walks west for 80 meters to a bench to feed some pigeons. She then walks north for another 30 meters to a concession stand. If Susie returns home in a straight line from the concession stand, how far will she walk from the concession stand to her house, in meters?
70
200
100
25
50
100
Susie walks 30 meters north, then 80 meters west, then 30 meters north again. Thus, she walks 60 meters north and 80 meters west. These two directions are 90 degrees away from one another.
At this point, construct a right triangle with one leg that measures 60 meters and a second leg that is 80 meters.
You can save time by using the 3:4:5 common triangle. 60 and 80 are 


We can solve for the length of the missing hypotenuse by applying the Pythagorean theorem:
Substitute the following known values into the formula and solve for the missing hypotenuse: side 
Susie will walk 100 meters to reach her house.
Example Question #83 : Triangles
The lengths of the sides of a triangle are consecutive odd numbers and the triangle's perimeter is 57 centimeters. What is the length, in centimeters, of its longest side?
25
21
17
23
19
21
First, define the sides of the triangle. Because the side lengths are consecutive odd numbers, if we define the shortest side will be as 
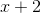

Substitute in the known values and variables.
Subtract 6 from both sides of the equation.
Divide both sides of the equation by 3.
Solve.
This is not the answer; we need to find the length of the longest side, or 
Substitute in the calculated value for 
The longest side of the triangle is 21 centimeters long.
Example Question #101 : Plane Geometry
Each of the following answer choices lists the side lengths of a different triangle. Which of these triangles does not have a right angle?


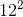

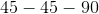
Example Question #1324 : Plane Geometry
Find the length of the hypotenuse.

Recall how to find the length of the hypotenuse, 
Substitute in the given values.
Simplify.
Solve.
Now, because we want to solve for just 
Simplify.
Example Question #71 : Plane Geometry
In the figure below, right triangle 




How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
First, we need to use the Pythagorean theorem to solve for 
Because we are dealing with a triangle, the only valid solution is 
After you have found 
Example Question #12 : Triangles
Find the perimeter of the triangle below.

How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem. The perimeter of a triangle is simply the sum of its three sides. Our problem is that we only know two of the sides. The key for us is the fact that we have a right triangle (as indicated by the little box in the one angle). Knowing two sides of a right triangle and needing the third is a classic case for using the Pythagorean theorem. In simple (sort of), the Pythagorean theorem says that sum of the squares of the lengths of the legs of a right triangle is equal to the square of the length of its hypotenuse.
Every right triangle has three sides and a right angle. The side across from the right angle (also the longest) is called the hypotenuse. The other two sides are each called legs. That means in our triangle, the side with length 17 is the hypotenuse, while the one with length 8 and the one we need to find are each legs.
What the Pythagorean theorem tells us is that if we square the lengths of our two legs and add those two numbers together, we get the same number as when we square the length of our hypotenuse. Since we don't know the length of our second leg, we can identify it with the variable 
This allows us to create the following algebraic equation:
which simplified becomes
To solve this equation, we first need to get the variable by itself, which can be done by subtracting 64 from both sides, giving us
From here, we simply take the square root of both sides.
Technically, 
But we aren't done yet. We now know the length of our missing side, but we still need to add the three side lengths together to find the perimeter.
Our answer is 40.
Example Question #3 : How To Find The Perimeter Of A Right Triangle
Given that two sides of a right triangle are 

How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
In order to calculate the perimeter we need to find the length of the hypotenuse using the Pythagorean theorem.
Rearrange.
Substitute in known values.
Now that we have found the missing side, we can substitute the values into the perimeter formula and solve.
Example Question #4 : How To Find The Perimeter Of A Right Triangle
Find the perimeter.

How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
Recall how to find the perimeter of a triangle:
The given triangle has 
Recall the Pythagorean theorem:
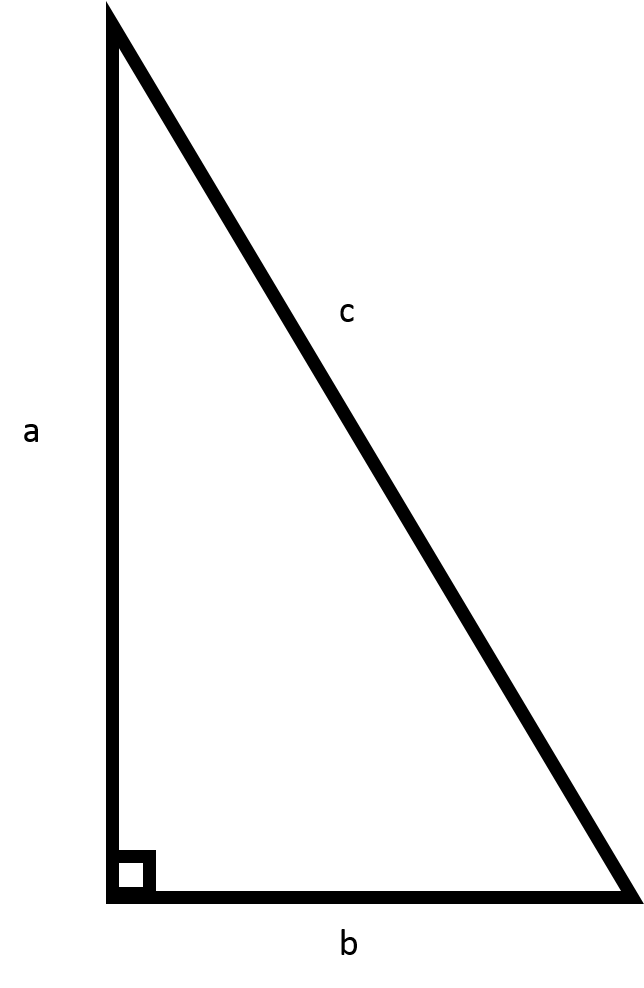
Since we are finding the length of side 
Plug in the values of 

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to 
Example Question #5 : How To Find The Perimeter Of A Right Triangle
Find the perimeter.

How do you find the perimeter of a right triangle?
There are three primary methods used to find the perimeter of a right triangle.
- When side lengths are given, add them together.
- Solve for a missing side using the Pythagorean theorem.
- If we know side-angle-side information, solve for the missing side using the Law of Cosines.
Method 1:
This method will show you how to calculate the perimeter of a triangle when all sides lengths are known. Consider the following figure:

If we know the lengths of sides 


Method 2:
In right triangles, we can calculate the perimeter of a triangle when we are provided only two sides. We can do this by using the Pythagorean theorem. Let's first discuss right triangles in a general sense. A right triangle is a triangle that has one 






If a triangle appears in this format, then we can use the Pythagorean theorem to solve for any missing side. This formula is written in the following manner:
We can rearrange it in a number of ways to solve for each of the sides of the triangle. Let's rearrange it to solve for the hypotenuse, 
Rearrange and take the square root of both sides.
Simplify.
Now, let's use the Pythagorean theorem to solve for one of the legs, 
Subtract 
Take the square root of both sides.
Simplify.
Last, let's use the Pythagorean theorem to solve for the adjacent leg, 
Subtract 
Take the square root of both sides.
Simplify.
It is important to note that we can only use the following formulas to solve for the missing side of a right triangle when two other sides are known:
After we find the missing side, we can use the perimeter formula to calculate the triangle's perimeter.
Method 3:
This method is the most complicated method and can only be used when we know two side lengths of a triangle as well as the measure of the angle that is between them. When we know side-angle-side (SAS) information, we can use the Law of Cosines to find the missing side. In order for this formula to accurately calculate the missing side we need to label the triangle in the following manner:

When the triangle is labeled in this way each side directly corresponds to the angle directly opposite of it. If we label our triangle carefully, then we can use the following formulas to find missing sides in any triangle given SAS information:
After, we calculate the right side of the equation, we need to take the square root of both sides in order to obtain the final side length of the missing side. Last, we need to use the perimeter formula to obtain the distance of the side lengths of the polygon.
Solution:
Now, that we have discussed the three methods used to calculate the perimeter of a triangle, we can use this information to solve the problem.
Recall how to find the perimeter of a triangle:
The given triangle has 
Recall the Pythagorean theorem:

Since we are finding the length of side 
Plug in the values of 

Now, plug in all three values into the equation to find the perimeter. Use a calculator and round to 
All Basic Geometry Resources
















































































































