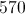AP Statistics : Univariate Data Descriptors
Study concepts, example questions & explanations for AP Statistics
All AP Statistics Resources
Example Questions
Example Question #1 : How To Find The Mean For A Set Of Data
Number Crunchers Inc. has offices in New York and Wisconsin. The mean salary for office workers in New Work is $28,500. The mean salary for office workers in the Wisconsin office is $22,500. The New York office has 128 office workers and the Wisconsin office has 32 office workers. What is the mean salary paid to the office workers in Number Crunchers Inc.?
The total amount paid in salaries to the office workers is
which is paid to 
Example Question #1 : How To Find The Mean For A Set Of Data
Six homes are for sale and have the following dollar values in thousands of dollars:
535
155
305
720
315
214
What is the mean value of the six homes?
The mean is calculated by adding all the values in a group together, then dividing the sum by the total number in the group. In this case, six homes are for sale. The six home values are added together 
Example Question #1 : How To Find The Range For A Set Of Data
Six homes are for sale and have the following dollar values in thousands of dollars:
535
155
305
720
315
214
What is the range of the values of the six homes?
The range is the simplest measurement of the difference between values in a data set. To find the range, one simply subtracts the lowest value from the greatest value, ignoring the others. Here, the lowest value is 155 and the greatest is 720.
Example Question #1 : How To Find The Range For A Set Of Data
Alice recorded the outside temperature at noon each day for one week. These were the results.
Monday: 78
Tuesday: 85
Wednesday: 82
Thursday: 84
Friday: 82
Saturday: 79
Sunday: 80
What is the range of temperatures?
The range is the simplest measurement of the difference between values in a data set. To find the range, simply subtract the lowest value from the greatest value, ignoring the others.
Example Question #1 : How To Find The Range For A Set Of Data
Find the range for the set.
To find the range, subtract the minimum value from the maximum value
minimum:
maximum:
So,
maximum - minimum =
Example Question #1 : How To Find The Range For A Set Of Data
A business tracked the number of customer calls received over a period of five days. What was the range of customer calls received daily?
Day 1: 57
Day 2: 63
Day 3: 48
Day 4: 49
Day 5: 59
The range is the simple measurement of the difference between values in a dataset.
To find the range, simply subtract the lowest value from the greatest value, ignoring the others.
Example Question #1 : How To Find The Range For A Set Of Data
Find the range for the set of data
The range is equal to the absolute difference between the minimum and maximum value.
We find the range to be
Example Question #2 : How To Find The Range For A Set Of Data
Let 
What is the range of the set.
To find the range, subtract the minimum value from the maximum value
minimum:
maximum:
So,
maximum - minimum =
Example Question #1 : How To Find The Interquartile Range For A Set Of Data
Find the interquartile range for the following data set:
To find the interquartile range, first find the median. This will split the data set into the upper and lower halves. The median for this data set is 11.
Focusing on the lower half, we can find the median, which is the first quartile, Q1:
Focusing on the upper half, we can find the median, which is the third quartile, Q3:
The interquartile range is just Q3 - Q1, in this case
Example Question #12 : Univariate Data Descriptors
Find the interquartile range for the following data set:
To find the interquartile range, first find the median. This will split the data set into the upper and lower halves. The median for this data set is 15.
Focusing on the lower half, we can find the median, which is the first quartile, Q1:
Focusing on the upper half, we can find the median, which is the third quartile, Q3:
The interquartile range is just Q3 - Q1, in this case
All AP Statistics Resources
