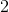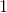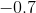All AP Statistics Resources
Example Questions
Example Question #2 : How To Find Outliers
Use the following five number summary to answer the question below:
Min:
Q1:
Med:
Q3:
Max:
Which of the following is true regarding outliers?
There is only one outlier in this entire data set.
There are no outliers in the upper side of the data set, but there is at least one outlier on the lower side of the data set.
There is at least one outlier in the lower side of the data set and at least one outlier in the upper side of the data set.
There are no outliers in this data set.
There are no outliers in the lower side of the data set, but there is at least one outlier on the upper side of the data set.
There is at least one outlier in the lower side of the data set and at least one outlier in the upper side of the data set.
Using the 

This allows us to determine that there is at least one outlier in the upper side of the data set and at least one outlier in the lower side of the data set. Without any more information, we are not able to determine the exact number of outliers in the entire data set.
Example Question #3 : How To Find Outliers
Which values in the above data set are outliers?
no outliers
Step 1: Recall the definition of an outlier as any value in a data set that is greater than 

Step 2: Calculate the IQR, which is the third quartile minus the first quartile, or 










Step 3: 

Example Question #1 : How To Find Outliers
A certain distribution has a 1st quartile of 8 and a 3rd quartile of 16. Which of the following data points would be considered an outlier?
An outlier is any data point that falls 





Example Question #1 : How To Create Residual Plots
On a residual plot, the 

independent variable; the dependent variable
dependent variable; residuals
residuals; the independent variable
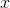

independent variable;
independent variable;
A residual plot shows the difference between the actual and expected value, or residual. This goes on the y-axis. The plot shows these residuals in relation to the independent variable.
Example Question #1 : How To Do Logarithmic Transformations
Example Question #1 : How To Do Logarithmic Transformations
What transformation should be done to the data set, with its residual shown below, to linearize the data?

multiply the independent variable by
take the log of the dependent variable
multiply the dependent variable by a constant k.
Add 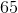
Nothing, the data set is already linear
take the log of the dependent variable
Taking the log of a data set whose residual is nonrandom is effective in increasing the correleation coefficient and results in a more linear relationship.
Example Question #1 : How To Interpret Dotplots
A basketball coach wants to determine if a player's height can be used to predict the number of points that player scores in a season. Before using a statistical test to determine the precise relationship of the variables, the coach wants a visual of the data to see if there is likely to be a relationship. Which of the following should the coach create?
Histogram
Bell curve
Bar chart
Z-score
Scatterplot
Scatterplot
A scatterplot is a diagram that shows the values of two variables and provides a general illustration of the relationship between them.
Example Question #1 : Graphing Data
Based on the scatter plot below, is there a correlation between the 

Yes; negative exponential relationship
Yes; positive linear relationship
No; there is no correlation
Yes; negative linear relationship
Yes; negative linear relationship
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
Example Question #2 : Graphing Data
Order the correlation coefficients to fit the order of the following graphs (two coefficients will not be used)


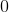





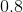
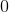


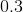


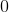


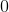
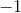



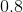
The first graph is random scatter, no correlation, the second is perfect linear, corellation 

Example Question #272 : Ap Statistics
Find the range of the data in the stem-and-leaf plot.
To find the range, subtract the minimum value from the maximum value
minimum:
maximum:
So,
maximum - minimum =
All AP Statistics Resources