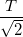All the energy that is stored up by the compressed spring needs to turn into gravitational potential energy for the stuntman to come to a rest 7.0 m in the air. Gravitational potential energy is modeled by the equation   and the energy in the spring system is modeled by the equation .  We can thus set these equations equal to one another:

We then rearrange the resulting equation for the compressed distance, which is :

Substituting in the given values, we can solve for :

We start with , where  is the point the mass is traveling to,  is the maximum displacement,  is , and  is the time it takes to travel the distance.

Rearranging this equation for  gives

Here,  is  because the point we're looking for is on the other side of the equilibrium point.

We compare the force from Hooke's Law to the force from gravity and solve for displacement:

Rearranging this equation to solve for , we get

Plugging in the given values, we get

Solving for , we get

When the spring is at its maximum compression, its potential energy is maximized and its kinetic energy is 0. When the mass is at the spring's equilibrium point, all of the potential energy is converted into kinetic energy, so kinetic energy is maximized (and equal to the maximum potential energy) and potential energy is 0. We set these two equations equal to each other and solve for velocity.

To find the equation for velocity, we take the first derivative of the position function. Don't forget the chain rule for the inside of the cosine!

To solve this problem, we can use the following equation:

Here,  is the period of an oscillation,  is the mass of the oscillating thing in kg, and  is the spring constant in .

Rearranging the equation to solve for the spring constant, , we get:

Plugging in the two known values, we get:

Solving for , we get .

Assuming this is a frictionless table, we don't have to take the work done by friction into account.

This is a conservation of energy problem. In this problem we have to realize that the potential energy of the spring at  is equal to the kinetic energy of the spring at + the potential energy of the spring at .

This can be shown in the following equation:

If we solve for , we get the following equation:

Remember to convert the distances given in centimeters to meters.

If we plug in all the variables, we get 

The correct answer is . Since the pendulum is at the bottom of its motion at this point, it has the lowest amount of energy given to gravitational potential and thus, the highest kinetic energy. 

Use the equation for the period of a simple pendulum:

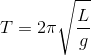
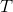
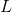
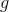
Here,  is the period in seconds,  is the length of the pendulum in meters, and  is the acceleration due to gravity in .

We can plug in the given quantities for length and acceleration to solve for the period.

Note that the mass of the rope as negligible. We also need not incorporate the extraneous information regarding the weight of the steel ball attached to the pendulum. This does not influence the period of this simple pendulum.

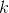
Because the springs are effectively in a parallel arrangement already, moving one does not change the effective spring constant, and therefore does not affect the period.