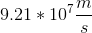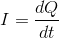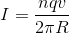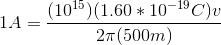All AP Physics C Electricity Resources
Example Questions
Example Question #1 : Current
A lamp has a 

Possible Answers:
Correct answer:
Explanation:
The formula for power is ,
Solve for the current, 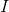
Example Question #65 : Electricity And Magnetism Exam
A particle accelerator with a radius of 500 meters can have up to 
How fast must the protons in the accelerator move in order to produce a current of 1A?
Possible Answers:
Correct answer:
Explanation:
The current produced is the total charge that circulates the particle accelerator per unit time.
We calculate this by the equation:
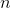



Using the given current, we then solve for the velocity:
All AP Physics C Electricity Resources
Popular Subjects
Reading Tutors in Philadelphia, ISEE Tutors in Chicago, GMAT Tutors in Boston, Algebra Tutors in Denver, ISEE Tutors in Washington DC, GMAT Tutors in San Francisco-Bay Area, French Tutors in Phoenix, GMAT Tutors in San Diego, GRE Tutors in San Diego, GMAT Tutors in Los Angeles
Popular Courses & Classes
SAT Courses & Classes in San Diego, GMAT Courses & Classes in Atlanta, SAT Courses & Classes in Seattle, GMAT Courses & Classes in Phoenix, ISEE Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Boston, GRE Courses & Classes in Washington DC, ISEE Courses & Classes in Denver, ISEE Courses & Classes in Seattle, MCAT Courses & Classes in Chicago
Popular Test Prep
ACT Test Prep in Washington DC, LSAT Test Prep in Seattle, ISEE Test Prep in Seattle, MCAT Test Prep in Philadelphia, MCAT Test Prep in Houston, LSAT Test Prep in Chicago, LSAT Test Prep in Dallas Fort Worth, GMAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Seattle, GMAT Test Prep in Houston