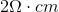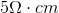Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics 2 : Resistivity

Study concepts, example questions & explanations for AP Physics 2

Create An Account

All AP Physics 2 Resources

6 Diagnostic Tests 149 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Resistivity

You have a 4cm long copper wire with a radius of 0.5mm. You have experimentally determined the resistance of the wire to be $0.8709m\Omega$ . What is the resistivity of copper?

Possible Answers:

$139.344\ \Omega \cdot m$

$0.011\Omega \cdot m$

$1.71\cdot10^{-8}\Omega\cdot m$

None of the other answers is correct

$18.5\cdot10^{-8}\Omega\cdot m$

Correct answer:

$1.71\cdot10^{-8}\Omega\cdot m$

Explanation:

The resistivity of a material is how much the material resists the flow of charge through it. Metals have low resistivities (which makes them good conductors), while things like glass or plastic have high resistivities.

The equation for resistivity is as follows:

$R=\frac{\rho L}{A}$

is the length of the wire, is the cross-sectional area, is the resistance, and $\rho$ is the resistivity. We have values for and , and we're given the radius of the wire so we can find , so we're trying to solve for $\rho$ . If we rearrange the equation, we end up with this:

$\frac{RA}{L}=\rho$

We're given the radius of the wire, so to find the area, we square the radius and multiply it by $\pi$ .

$A=\pi r^2$

$A=\pi (0.0005)^2$

$A=7.854\cdot 10^{-7}$

Now, we can plug in our values.

$\frac{RA}{L}=\rho$

$\frac{(0.8709\cdot 10^{-3}) \cdot (7.854\cdot 10^{-7})}{0.04}=\rho$

$1.71\cdot 10^{-8}=\rho$

Therefore, the answer is $1.71\cdot10^{-8}\Omega\cdot m$ .

Report an Error

Example Question #2 : Resistivity

You create a cylinder of an unknown material that has a diameter of 2cm , and a height of 1cm . You attach the electrodes to the faces of the cylinder and find the sample has a resistance of $25\Omega$ .

What is the resistivity of the material?

Possible Answers:

$35\Omega \cdot cm$

$58.5\Omega \cdot cm$

$78.5\Omega \cdot cm$

$31.0\Omega \cdot cm$

$69.5\Omega \cdot cm$

Correct answer:

$78.5\Omega \cdot cm$

Explanation:

Use the equation for resistivity:

$R= \rho \frac{L}A{}$

First, find the cross sectional area.

$A=\pi r^{2}$

A=3.14cm^2

Plug in known values.

$R= \rho \frac{L}A{}$

$\rho = \frac{25\Omega\cdot 3.14cm^2}{1cm}$

$\rho =78.5\Omega \cdot cm$

Report an Error

Example Question #1 : Resistivity

You have a sample that is a cube of volume 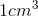1cm^3 . You attach electrodes to opposite faces and find the resistance to be $3\Omega$ .

What is the resistivity of the material?

Possible Answers:

$1\Omega \cdot cm$

$2\Omega \cdot cm$

$3\Omega \cdot cm$

$5\Omega \cdot cm$

$4\Omega \cdot cm$

Correct answer:

$3\Omega \cdot cm$

Explanation:

Since we have a cube of volume 1cm^3 , the length of the material must be 1cm . Use the equation for resistivity.

$R=\rho \frac{L}{A}$

Rearrange the equation and plug in known values.

$\rho = \frac{RA}{L}$

$\rho=\frac{3\Omega\cdot 1cm^2}{1cm}=3\Omega\cdot cm$

Report an Error

Example Question #3 : Resistivity

You have a material with resistivity $3500\Omega\cdot m$ . You build a component of a fuel cell out of this material with a cross sectional area of 0.01m^2 , and a thickness of 0.01m .

What will be the resistance of this component?

Possible Answers:

$3.5\Omega$

$350\Omega$

$3500\Omega$

None of these

$0.35\Omega$

Correct answer:

$3500\Omega$

Explanation:

Use the resistivity equation:

$R= \rho \frac{L}{A}$

$R= 3500\Omega \cdot m \cdot \frac{0.01m}{0.01m^2}$

$R=3500\Omega$

Report an Error

Example Question #48 : Circuits

You are researching new materials for usage in spacecraft electronics.

You have a new material, known as "Type F."

You carve out a cylinder of the material. It is 4.5 cm tall, with a radius of 2.65 cm .

You put electrodes on each face of the cylinder.

You determine the resistance to be $935\Omega$ .

What is the resistivity of "Type F?"

Possible Answers:

None of these

$45.8\Omega\cdot meters$

$30.9 \Omega\cdot meters$

$39.1 \Omega\cdot meters$

$12.1 \Omega\cdot meters$

Correct answer:

$45.8\Omega\cdot meters$

Explanation:

We will use the relationship

$\rho=R\frac{A}{l}$

Where $\rho$ is the resistivity, is the resistance, is the surface area of the face the current is coming in or out of, and is the length from one face to the other.

Remember that the area of a circle is

$A=\pi\cdot r^2$

Combining our equations we get

$\rho=R\frac{\pi\cdot r^2}{l}$

We then need to plug in our values

$\rho=935\frac{\pi\cdot{.0265}^2}{.045}$

$45.8\Omega\cdot meters=\rho$

Report an Error

Example Question #862 : Ap Physics 2

You are researching new materials for usage in spacecraft electronics.

You have a new material, known as "Type G."

You carve out a cylinder of the material. It is 2.5 cm tall, with a radius of 1.5 cm .

You put electrodes on each face of the cylinder.

You determine the resistance to be 9.53 ohms .

What is the resistivity of "Type G?"

Possible Answers:

None of these

$2.70\times10^{-3}\Omega\cdot meters$

$4.45\times10^{-3}\Omega\cdot meters$

$1.3\times10^{3}\Omega\cdot meters$

$1.9\times10^{-3}\Omega\cdot meters$

Correct answer:

$2.70\times10^{-3}\Omega\cdot meters$

Explanation:

We will use the relationship

$\rho=R\frac{A}{l}$

Where $\rho$ is the resistivity, is the resistance, is the surface area of the face the current is coming in or out of, and is the length from one face to the other.

Remember that the area of a circle is

$A=\pi\cdot r^2$

Combining our equations we get

$\rho=R\frac{\pi\cdot r^2}{l}$

We then need to plug in our values

$\rho=9.53\frac{\pi\cdot .015^2}{.025}$

$2.70\times 10^{-3}\Omega\cdot meters=\rho$

Report an Error

Example Question #1 : Resistivity

You are researching new materials for usage in spacecraft electronics.

You have a new material, known as "Type Z."

You carve out a cylinder of the material. It is 2.2 cm tall, with a radius of .2 cm .

You put electrodes on each face of the cylinder.

You determine the resistance to be .22 ohms .

What is the resistivity of "Type Z?"

Possible Answers:

$1.75\times 10^{-4} \Omega\cdot meters$

$1.26\times 10^{-4}\Omega\cdot meters$

$1.11\times 10^{-4}\Omega\cdot meters$

None of these

$1.99\times 10^{-4} \Omega\cdot meters$

Correct answer:

$1.26\times 10^{-4}\Omega\cdot meters$

Explanation:

We will use the relationship

$\rho=R\frac{A}{l}$

Where $\rho$ is the resistivity, is the resistance, is the surface area of the face the current is coming in or out of, and is the length from one face to the other.

Remember that the area of a circle is

$A=\pi\cdot r^2$

Combining our equations we get

$\rho=R\frac{\pi\cdot r^2}{l}$

We then need to plug in our values

$\rho=.22\frac{\pi\cdot.002^2}{.022}$

$\rho=1.26\times10^{-4}\Omega\cdot meters$

Report an Error

Example Question #1 : Resistivity

A researcher is testing the electrical properties of a circuit that contains a resistor of unknown material. The resistor is a 3cm cylinder with a radius of 0.5cm . The researcher measures the resistance of the resistor to be $0.3\Omega$ . What is the resistivity of this unknown material?

Possible Answers:

$3.75\Omega\cdot m$

$7.85*10^{-4}\Omega\cdot m$

$8.75*10^{-3}\Omega\cdot m$

$9.1*10^{-4}\Omega\cdot m$

$1.6*10^{-2}\Omega\cdot m$

Correct answer:

$7.85*10^{-4}\Omega\cdot m$

Explanation:

Use the equation for resistivity:

$\rho=R\frac{A}{L}$

Here, $\rho$ is the resistivity, is the resistance, is the cross-sectional area, and is the length of the resistor.

Begin by finding the cross-sectional area of the material, which is circular:

$A=\pi r^2$

$A=\pi (0.005m)^2$

$A\approx 0.0000785m^2$

Now plug in all known values and solve for resistivity.

$\rho=0.3\Omega*\frac{0.0000785m^2}{0.03m}$

$\rho = 0.000785\Omega\cdot m$

$\rho = 7.85*10^{-4}\Omega\cdot m$

Report an Error

Example Question #1 : Resistivity

A scientist carves out a cylinder of a new material she developed. It is 4.5 cm tall, with a radius of .60 cm . She put electrodes on each face of the cylinder. She determined the resistance to be $.75\Omega$ . What is the resistivity of this material?

Possible Answers:

$3.70 *10^{ -3} \Omega \cdot m$

None of these

$1.88 *10^{-3} \Omega\cdot m$

$4.50 *10^{ -3} \Omega \cdot m$

$1.70 *10^{ -3} \Omega \cdot m$

Correct answer:

$1.88 *10^{-3} \Omega\cdot m$

Explanation:

Use the relationship:

$\rho =R\frac{A}{l}$

Here, $\rho$ is the resistivity, is the resistance, is cross sectional area, and is the length.

The area of a circle is:

$A=\pi r^2$

Substitute:

$\rho =R\frac{\pi r^2}{l}$

Plug in given values and solve

$\rho =.75\Omega \frac{\pi (.006m)^2}{.045m}$

$\rho = 1.88 *10^{-3} \Omega\cdot m$

Report an Error

Example Question #5 : Resistivity

There is a sample of an unknown material under testing. It is 4.75 cm tall, with a radius of .65 cm . Electrodes are placed on each face of the cylinder. It is determined that the resistance to 10.5 ohms .

What is the resistivity?

Possible Answers:

$.0375 \Omega*meters$

$.0333 \Omega*meters$

$.0293 \Omega*meters$

None of these

$.0750 \Omega*meters$

Correct answer:

$.0293 \Omega*meters$

Explanation:

Using the relationship

$\rho=R\frac{A}{l}$

Where $\rho$ is the resistivity, is the resistance, is the cross sectional area, and is the length from one face to the other.

The area of a circle is

$A=\pi*r^2$

Combining equations

$\rho=R\frac{\pi*r^2}{l}$

Plugging in values

$\rho=10.5\frac{\pi*.0065^2}{.0475}$

$.0293 \Omega*meters=\rho$

Report an Error

View Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View Tutors

Satweka
Certified Tutor

The University of Texas at Dallas, Master of Science, Biomedical Engineering.

View Tutors

Tonja
Certified Tutor

McNeese State University, Bachelor in Arts, English.

All AP Physics 2 Resources

6 Diagnostic Tests 149 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

English Tutors in Boston, Chemistry Tutors in Seattle, Reading Tutors in San Diego, Reading Tutors in Dallas Fort Worth, GMAT Tutors in Seattle, SSAT Tutors in Phoenix, Math Tutors in Miami, ACT Tutors in Philadelphia, ACT Tutors in San Francisco-Bay Area, Chemistry Tutors in Atlanta

Popular Courses & Classes

ACT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in San Diego, Spanish Courses & Classes in San Diego, SAT Courses & Classes in Boston, SAT Courses & Classes in Washington DC, Spanish Courses & Classes in Atlanta, ISEE Courses & Classes in Houston, ACT Courses & Classes in San Diego, SSAT Courses & Classes in Phoenix, SSAT Courses & Classes in Washington DC

Popular Test Prep

GMAT Test Prep in Washington DC, SAT Test Prep in Boston, MCAT Test Prep in Atlanta, SSAT Test Prep in Atlanta, GMAT Test Prep in San Diego, MCAT Test Prep in Philadelphia, SSAT Test Prep in Seattle, ACT Test Prep in San Diego, ACT Test Prep in Chicago, MCAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics 2 : Resistivity

Study concepts, example questions & explanations for AP Physics 2

All AP Physics 2 Resources

Example Questions

Example Question #1 : Resistivity

Example Question #2 : Resistivity

Example Question #1 : Resistivity

Example Question #3 : Resistivity

Example Question #48 : Circuits

Example Question #862 : Ap Physics 2

Example Question #1 : Resistivity

Example Question #1 : Resistivity

Example Question #1 : Resistivity

Example Question #5 : Resistivity

All AP Physics 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: