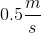Call Now to Set Up Tutoring:

(888) 888-0446

AP Physics 2 : Fluid Dynamics

Study concepts, example questions & explanations for AP Physics 2

Create An Account

All AP Physics 2 Resources

6 Diagnostic Tests 149 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 Next →

Example Question #6 : Turbulence

Honey is flowing through a rectangular duct with width w = 2.2m at a velocity of $0.8\frac{m}{s}$ . What is the depth of the honey if the Reynold's number is 150 ?

$\rho_h = 1,420\frac{kg}{m^3}$

$\mu_h = 10Pa\cdot s$

Possible Answers:

21cm

1.3m

96cm

1.8m

47cm

Correct answer:

47cm

Explanation:

We will use the expression for Reynold's number for this problem:

$Re = \frac{\rho_w vD_H}{\mu_w}$

Rearranging for hydraulic diameter, we get:

$D_H = \frac{Re\mu_w}{\rho_wv}$

For a partially filled rectangular duct, the expression for hydraulic diameter is:

$D_H = \frac{4hw}{2h+w}$

$\frac{4hw}{2h+w} = \frac{Re\mu_w}{\rho_wv}$

Rearranging for height:

$4hw = \left (\frac{Re\mu_w}{\rho_wv} \right )(2h+w)$

$h\left (4w -\frac{2Re\mu_w}{\rho_wv} \right )= \left (\frac{Re\mu_w}{\rho_wv} \right )w$

$h= \frac{\left (\frac{wRe\mu_w}{\rho_wv} \right )}{\left (4w -\frac{2Re\mu_w}{\rho_wv} \right )}$

h = 47cm

Report an Error

Example Question #81 : Fluids

By what factor does the Reynolds's number change for water flowing through a circular tube as the cross-sectional area of the tube gradually triples?

Possible Answers:

0.77

1.3

1.0

1.7

0.58

Correct answer:

0.58

Explanation:

Let's begin with the expression for Reynold's number:

$Re_1 = \frac{\rho v_1D_{H_{1}}}{\mu}$

$Re_2= \frac{\rho v_2D_{H_{2}}}{\mu}$

Dividing the second expression by the first, we get:

$\frac{Re_2}{Re_1}= \frac{\left (\frac{\rho v_2D_{H_{2}}}{\mu} \right )}{\left (\frac{\rho v_1D_{H_{1}}}{\mu} \right )}$

$\frac{Re_2}{Re_1}= \frac{v_2D_{H_{2}}}{v_1D_{H_{1}}}$ (1)

From the problem statement, we are told:

3A_1 = A_2

$3\frac{\pi D_1^2}{4}=\frac{\pi D_2^2}{4}$

$D_2 = \sqrt{3}D_1$

Also, for a circular tube:

D_H = D

Therefore:

$D_{H_{2}}=\sqrt{3}D_{H_{1}}$ (2)

Now we need to determine the change in velocity. From the law of continuity, we know that:

$\dot{V_1}=\dot{V_2}$

v_1A_1 = v_2A_2

Rearranging:

$v_2 = v_1\frac{A_1}{A_2}$

Where:

3A_1=A_2

Thus:

$v_2=\frac{v_1}{3}$ (3)

Plugging in expressions (2) and (3) into (1), we get:

$\frac{Re_2}{Re_1}= \frac{\sqrt{3}v_1D_{H_{1}}}{3v_1D_{H_{1}}}$

$\frac{Re_2}{Re_1}=\frac{\sqrt{3}}{3}$

$\frac{Re_2}{Re_1}= 0.58$

Report an Error

Example Question #1 : Turbulence

A baseball is thrown at a catcher with a high velocity and the ball passes right by the glove of the catcher. Which of the following scenarios will occur because of this?

Possible Answers:

The ball will be pushed away from glove because of the decreased air pressure.

The ball will be pushed away from glove because of the increased air pressure.

The ball will be pulled toward the glove because of the increased air pressure.

The ball will be pulled toward the glove because of the decreased air pressure.

None of these situations will occur.

Correct answer:

The ball will be pulled toward the glove because of the decreased air pressure.

Explanation:

As the baseball passes by the glove, the air surrounding the glove increases in velocity. The increase in air velocity will cause a decrease in pressure. The decrease in pressure causes the ball to be pulled towards the glove.

Therefore the correct answer is that the ball will be pulled toward the glove because of the decreased air pressure.

Report an Error

Example Question #81 : Fluids

Water flows through a tube with a diameter of 2m at a rate of $800 \frac{kg}{s}$ . What is the velocity of the water?

$\rho_{water} = 1\frac{kg}{l}$

Possible Answers:

$0.75\frac{m}{s}$

$0.25\frac{m}{s}$

$1.0\frac{m}{s}$

$0.62\frac{m}{s}$

$0.5\frac{m}{s}$

Correct answer:

$0.25\frac{m}{s}$

Explanation:

The velocity of the water can be determined from the following formula:

$v = \frac{\dot{V}}{A}$

We need to calculate the volumetric flow rate and the cross-sectional area. For the flow rate:

$\dot m = \dot V \cdot \rho_{water}$

Rearrange to solve for volumetric flow rate:

$\dot V = \frac{\dot m}{\rho_{water}} = \frac{800\frac{kg}{s}}{1000\frac{kg}{m^3}} = 0.8 \frac{m^3}{s}$

Next, calculate cross-sectional area:

$A = \pi \frac{d^2}{4} = \pi \frac{(2m)^2}{4} = \pi m^2$

Now we can solve for the velocity:

$v = \frac{0.8\frac{m^3}{s}}{\pi m^2} = 0.25 \frac{m}{s}$

Report an Error

Example Question #2 : Flow Rate

Suppose that water flows from a pipe with a diameter of 1m into another pipe of diameter 0.5m. If the speed of water in the first pipe is $5\: \frac{m}{s}$ , what is the speed in the second pipe?

Possible Answers:

$20 \frac{m}{s}$

$10 \frac{m}{s}$

$2.5 \frac{m}{s}$

$5 \frac{m}{s}$

Correct answer:

$20 \frac{m}{s}$

Explanation:

To find the answer to this question, we'll need to use the continuity equation to determine the flow rate, which will be the same in both pipes.

vA=f

$v_{1}A_{1}=v_{2}A_{2}$

We'll also need to calculate the area of the pipe using the equation:

$A=\pi r^{2}$

$A_{1}=\pi r_{1}^{2}=\pi (0.5\m)^{2}=0.25\pi m^{2}$

$A_{2}=\pi r_{2}^{2}=\pi \left ( 0.25 m\right )^{2}=0.0625\pi m^{2}$

Solve the combined equation for v_2 and plug in known values to find the velocity of the water through the second pipe.

$v_{2}=\frac{v_{1}A_{1}}{A_{2}}$

$v_{2}=\frac{(5 \frac{m}{s})(0.25\pi m^{2})}{0.0625\pi m^{2}}=20 \frac{m}{s}$

Report an Error

Example Question #81 : Fluids

A diameter garden hose with a diameter of 3cm sprays water travels through a hose at $1\frac{m}{s}$ . At the end of the garden hose, the diameter reduces to 2cm. What is the speed of the water coming out at the end?

Possible Answers:

$2 \frac{m}{s}$

$2.25 \frac{m}{s}$

$2.75 \frac{m}{s}$

$1.5 \frac{m}{s}$

$0.67 \frac{m}{s}$

Correct answer:

$2.25 \frac{m}{s}$

Explanation:

Use the continuity equation for incompressible fluids.

A_1v_1 =A_2v_2

The cross sectional area of the garden hose at both ends are circular regions. Rewrite the equation replacing areas with the formula for an area of a circle and solve for the velocity at the second point.

$\left(\frac{\pi d_1^2}{4}\right)v_1 =\left(\frac{\pi d_2^2}{4}\right)v_2$

$v_2 = \frac{v_1 d_1^2}{d_2^2}= \frac{1\frac{{m}}{{s}}(3^2)}{2^2}= \left(\frac{3}{2}\right)^2=2.25 \frac{{m}}{{s}}$

Report an Error

Example Question #1 : Flow Rate

An civil engineer is designing the outflow of a pond. The pond has a radius of r=200m , and the maximum sustained rainfall rate is $v=2.1*10^{-5}\frac{m}{s}$ , about 3 inches per hour. If the engineer makes the outflow with a cross-sectional area of A=0.5 m^2 , what maximum velocity will the outflow of water have during a heavy rainstorm if the surface level of the pond does not change?

Possible Answers:

$v=8.4*10^{-3}\frac{m}{s}$

$v=5.56\frac{m}{s}$

$v=8.8\frac{m}{s}$

$v=16\frac{m}{s}$

$v=4.2*10^{-3}\frac{m}{s}$

Correct answer:

$v=5.56\frac{m}{s}$

Explanation:

This is a volume flow rate problem. Because the water is an incompressible fluid, we can apply the flow rate equation:

$A_{1}* v_{1}=A_{2}* v_{2}$

Find the surface area of the pond:

$A_{1}=\pi r^2 = 3.14* 200^2 =1.3* 10^5m^2$

Substitute into the flow rate equation:

$1.3*10^5 * 2.1*10^{-5}=0.5* v_2$

$v_2=5.56\frac{m}{s}$

Report an Error

Example Question #5 : Flow Rate

An incompressible fluid flows through a pipe. At location 1 along the pipe, the volume flow rate is $10 \frac{m^3}{s}$ . At location 2 along the pipe, the area halves. What is the volume flow rate at location 2?

Possible Answers:

$5 \frac{m^3}{s}$

$10 \frac{m^3}{s}$

$4 \frac{m^3}{s}$

$20 \frac{m^3}{s}$

Correct answer:

$10 \frac{m^3}{s}$

Explanation:

When the area halves, the velocity of the fluid will double. However, the volume flow rate (the product of these two quantities) will remain the same. In other words, the volume of water flowing through location 1 per second is the same as the volume of water flowing through location 2 per second.

Report an Error

Example Question #6 : Flow Rate

What is the volumetric flow rate of oil in a 12m diameter pipe? The velocity of the oil is $5\frac{m}{s}$ .

Possible Answers:

$Q=60\frac{m^3}{s}$

$Q=124.7\frac{m^3}{s}$

$Q=226.5\frac{m^3}{s}$

$Q=565.2\frac{m^3}{s}$

Correct answer:

$Q=565.2\frac{m^3}{s}$

Explanation:

The volumetric flow rate of fluid is found using the equation:

Q=v*a

Where is the velocity of the fluid and is the cross-sectional area of the space through which the fluid is flowing.

In this problem the cross-section of the pipe is a circle. The area of the cross-section is:

$a=\pi*r^{2}=\pi*\left ( \frac{12}{2} \right )^{2}\approx113.04m^2$

The volumetric flow rate is:

$Q=v*a=5*113.04=565.2\frac{m^3}{s}$

Report an Error

Example Question #1 : Flow Rate

What is the volumetric flow rate of ethanol flowing through a square pipe with sidelength 4m? The velocity of the ethanol is $7\frac{m}{s}$ .

Possible Answers:

$Q=112\frac{m^3}{s}$

$Q=28\frac{m^3}{s}$

$Q=213\frac{m^3}{s}$

$Q=68\frac{m^3}{s}$

Correct answer:

$Q=112\frac{m^3}{s}$

Explanation:

The volumetric flow rate of fluid is found using the equation:

Q=v*a

Where is the velocity of the fluid and is the cross-sectional area of the space through which the fluid is flowing.

In this problem the cross-section of the pipe is a square. The area of the cross-section is:

a=4*4=16m^2

The volumetric flow rate is:

$Q=v*a=7*16=112\frac{m^3}{s}$

Report an Error

← Previous 1 2 3 4 5 6 Next →

View Tutors

Monica
Certified Tutor

Purdue University-Main Campus, Bachelor of Science, Mathematics Teacher Education. Concordia University-Ann Arbor, Master of ...

View Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

View Tutors

Stephen
Certified Tutor

University of Hull, Bachelor of Science, Physical Chemistry.

All AP Physics 2 Resources

6 Diagnostic Tests 149 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Miami, Biology Tutors in Denver, Biology Tutors in Los Angeles, Reading Tutors in San Diego, Computer Science Tutors in Chicago, Calculus Tutors in Philadelphia, Chemistry Tutors in New York City, Calculus Tutors in Houston, Calculus Tutors in Phoenix, Algebra Tutors in Atlanta

Popular Courses & Classes

GRE Courses & Classes in Phoenix, SAT Courses & Classes in Philadelphia, LSAT Courses & Classes in Phoenix, LSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Houston, SSAT Courses & Classes in Miami, ISEE Courses & Classes in Miami, ISEE Courses & Classes in New York City, Spanish Courses & Classes in Chicago, ACT Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in Philadelphia, GRE Test Prep in Los Angeles, MCAT Test Prep in Boston, GMAT Test Prep in Los Angeles, MCAT Test Prep in Phoenix, ISEE Test Prep in Dallas Fort Worth, SAT Test Prep in Washington DC, MCAT Test Prep in Denver, ISEE Test Prep in Denver, ISEE Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Physics 2 : Fluid Dynamics

Study concepts, example questions & explanations for AP Physics 2

All AP Physics 2 Resources

Example Questions

Example Question #6 : Turbulence

Example Question #81 : Fluids

Example Question #1 : Turbulence

Example Question #81 : Fluids

Example Question #2 : Flow Rate

Example Question #81 : Fluids

Example Question #1 : Flow Rate

Example Question #5 : Flow Rate

Example Question #6 : Flow Rate

Example Question #1 : Flow Rate

All AP Physics 2 Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: