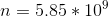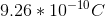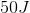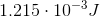As D increases, C will decrease

Does the battery matter? No. Capacitance is a "geometric" quantity. This means that it can be determined solely by physical parameters like the area and separation distance. The charge on the plates, voltage difference, electric field and any other quantity you could think of does not influence the capacitance other than A or D. 

The voltage rise through the source must be the same as the drop through the capacitor.

The voltage drop across the capacitor is the equal to the electric field multiplied by the distance.

Combine equations and find the electric field:

Convert mm to m and plugg in values:

Use the electric field in a capacitor equation:

Convert  to  and plug in values:

The magnitude of total charge on the positive plate is equal to the total charge on the negative plate, so to find the number of excess elections:

The voltage rise through the source must be the same as the drop through the capacitor.

The voltage drop across the capacitor is the equal to the electric field multiplied by the distance.

Combine equations and solve for the electric field:

Convert mm to m and plug in values:

Using the electric field in a capacitor equation:

Rearrange to solve for the charge:

Convert  to  and plug in values:

Voltage difference  is given by

, where  is the electric field strength and  is the distance between the two plates. 

For this problem,

The formula for capacitance  is given by:

,

Where  is dielectric strength,  is distance between plates,  is permittivity of empty space, and  is cross sectional area. 

To determine , we do

 because between the plates is a vacuum.

Putting it all together,

In parallel branches of a circuit, the voltage drops are all the same. Therefore, we know that the voltage drop across C3 is also 5V.

We can then use the following equation to calculate the total stored energy:

Since the voltage is the same for both capacitors, we can simply add the two capacitances to do one calculation for energy:

To find the amount of energy stored in a capactior, we use the equation

.

We're given the capacitance (), and the voltage (), so we'll use the third equation.

The equation for energy stored in a capacitor is 

We can find the capacitance by adding the capacitors together, and we have the voltage, so we'll use the second equation, .

When adding capacitors, remember how to add in series and parallel.

Capacitors  and  are in series,  and  are in parallel, and  and  are in parallel.

Now that we have the total capacitance, we can use the earlier equation to find the energy.

The total energy stored is 121.5J. 

In this circuit, the voltage source,  and , and  are all in parallel, meaning they share the same voltage.

To find the energy, we can use the formula

, with  being the energy,  being the capacitance, and being the voltage drop across that capacitor.

To use the formula we need the voltage across .

Another hint we can use is that  and  having the same charge since they're in series. First let's find the equivalent capacitance:

Now, we can use the formula 

 to calculate charge in the capacitor.

Now that we know a charge of  exists in both capacitors, we can use the formula again to find the voltage in only .

Finally, we plug this  into the first equation to calculate energy.

Equations required:

We see from the first equation the when D is doubled, C will be halved (since  and  are constant). From the third equation, we seed that when C is halved, the potential energy, U will double.