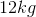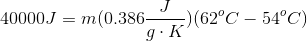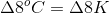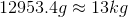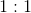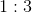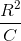The relationship between frequency and energy is determined by Planck's constant in a direct relationship. This means that as frequency increases, energy increases as well.

The electromagnetic waves with the highest frequency will have the greatest energy per photon, and vice versa.

In the electromagnetic spectrum, radio waves have the lowest frequency (largest wavelength) and gamma rays have the highest frequency (shortest wavelength). Gamma rays will thus have the highest frequency and greatest energy.

The amplitudes of in-phase waves add in what is called constructive interference. We can find the resultant amplitude of the first two waves by adding their individual amplitudes.

The third wave is out of phase, meaning that it will contribute destructive interference when the three waves align. We subtract the amplitude of the third wave from the total of the first two.

This is the final amplitude of the resultant wave.

Specific heat is most commonly applied in the equation to determine the heat required/released during a temperature change:

Rearranging this equal, we can see that this units of specific heat are units of heat per units of mass times units of temperature.

Heat energy can have the units of Joules or calories. Mass can have units of grams or kilograms. Temperature can have units of Kelvin, degrees Celsius, or degrees Fahrenheit. British thermal units (Btu) is a less common unit of heat, defined by the amount of heat required to raise one pound of water by one degree Fahrenheit.

Newtons are a unit of force, and cannot be used in the units for specific heat.

Our equation for temperature change using specific heat is:

Since Celsius and Kelvin use the same interval scale, we do not need to convert to find the change in temperature. Using the initial and final temperatures, the energy input, and the specific heat of copper, we can calculate the mass of copper present.

To simplify, we will solve for the temperature change separately.

Since the scale for Celsius and Kelvin is the same, this change is the same in either scale.

Use this value back in the original calculation.

Convert to kilograms to simplify.

You can simplify this question tremendously by using the definition of a dielectric constant. Dielectric constant is defined as the ratio of the electrostatic force in vacuum to the electrostatic force in the medium (in this case glass).

The question is asking for the reciprocal of this value: the ratio of the force in glass to the force in the vacuum. Our answer is calculated by taking the reciprocal of the dielectric constant of glass.

Moving a charge along an equipotential surface will involve no work done by the electric field. The potential is constant throughout an equipotential surface; therefore, the potential difference experienced by the electron will be zero. Remember that energy is dependent on the potential difference.

If the potential difference is zero then the energy (and work) will be zero.

This question is very simple if you realize that the force experienced by both charges is equal.

The definition of the two electrostatic forces are given by Coulomb's law:

In this question, we can rewrite this equation in terms of our given system.

It doesn’t matter if the charges of the two particles are different; both particles experience the same force because the charges of both particles are accounted for in the electrostatic force equation (Coulomb's law). This conclusion can also be made by considering Newton's third law: the force of the first particle on the second will be equal and opposite the force of the second particle on the first.

Since the forces are equal, their ratio will be .

The definition of a time constant for an RC circuit is the product of resistance and charge:

This is defined as the time it takes the capacitor to reach a charge that is around 63% of the maximum charge. It is also the time it takes to discharge around 37% of the charge. This value is commonly used to determine the amount of charge a capacitor has or the amount of current flowing through the capacitor at any given time point.

Recall the equation for potential energy in terms of capacitance:

According to the equation above, an increase in capacitance will lead to decrease in the amount of energy stored. This means that a larger capacitor will store less energy; therefore, statement I is false.

Any circuit elements connected in parallel will always have the same voltage drop. This applies to resistors, capacitors, and inductors. Statement II is true.

Remember that capacitance is defined as follows:

In this equation, is the area of the plates and  is distance between the plates. Increasing  will lead to a decrease in capacitance; therefore, statement III is false.

To solve this problem, you need to use the following two equations:

By substituting into the second equation you can write the change in potential energy in terms of voltage and charge.

Rearranging the previous equation will allow us to solve for the voltage.

Use the given values for stored potential energy and charge to solve for the voltage.