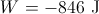All AP Physics 1 Resources
Example Questions
Example Question #142 : Newtonian Mechanics
A horizontal spring is oscillating with a mass sliding on a perfectly frictionless surface. If the amplitude of the oscillation is 


None of these
Using conservation of energy:
Plugging in values:
Solving for
Example Question #1 : Conservation Of Energy
A rollercoaster cart with a total mass of 1,000kg is at the top of a hill moving at 
This question covers the conservation of energy:
From the problem statement, we know that the cart has both initial potential and kinetic energy. We can assume that there is no final potential energy. This means that there is final kinetic energy from the final velocity that we are trying to find.
After eliminating final potential energy, we can rewrite the equation as:
We can eliminate mass from the equation to get:
We are solving for final velocity, so rearranging, we get:
Values for each variable were given in the problem statement, so we can simply plug in these values to solve:
Example Question #2 : Conservation Of Energy
A group of ten friends, each of mass 50kg, want to test the strength of a trampoline. At their highest jump, each friend is 2m above the trampoline. They all land on the trampoline at the same time and decelerate at a constant rate to a point of zero velocity over a period of 0.5s. The trampoline has a threshold of 5000N, above which it breaks. Do the friends succeed in breaking their trampoline?
Neglect air resistance and the distance the trampoline sags as a result of the friends landing.
No; they exert a force of
No; they exert a force of
Yes; they exert a force of
More information is required to solve
Yes; they exert a force of
Yes; they exert a force of
According to the problem statement, we can treat the friends as a single mass of 500kg. We can use the expression for conservation of energy to calculate the velocity as they hit the trampoline.
If we take the initial state to be when the friends are at their highest point and the final state to be when the friends hit the trampoline, we can rewrite:
Substituting in expressions:
Rearranging for velocity:
Plugging in our values:
The statement says that the friends decelerate from this velocity to zero over a period of 0.5 seconds. Therefore, we can write:
We can use this to calculate the force that the trampoline is exerting on the friends:
This is above the threshold of 5000 N, so the trampoline does break.
Example Question #2 : Conservation Of Energy
For a baseball field, the distance between home plate and the center field wall is about 





Neglect air resistance and assume
None of the other answers
There are two ways to solve this problem. The first uses the concept of conservation of energy, and the second uses kinematics. We'll go through both methods, as you should be comfortable using either one, as some problems won't have the ability to be easily solved using two different methods.
Method 1: Conservation of Energy
Note: The only reason we can use this method is because we know the height at which the ball crosses over the center field wall. Without that height, we would have to do method 2.
We will first split the initial velocity of the ball into its components:
Since we are neglecting air resistance, the x-component stays constant. Therefore we can say:
We can find the final y-componenet using our conservation of energy equation:
Substituting in our expressions:
Canceling out mass and rearranging for final velocity:
Note that this is one of the big five kineamtics equations with which you should be familiar. Plugging in our values, we get:
Now that we have the components, we can combine them to get the final velocity:
Method 2: Kinematics
We start off the same way by separating the velocities into their components:
Since we are neglecting air resistance, the x-component stays constant. Therefore we can say:
We also know how far the ball travels horizontally, so we can find out long it takes to cover that distance:
We can then use this time to find out the final vertical velocity:
The acceleration is subtracted because the acceleration is technically negative.
The velocity is negative because the ball is now traveling back downward. We can now combine the component velocities into the final velocity of the ball:
Example Question #3 : Work, Energy, And Power
A 

Each time the ball bounces, 10% of the kinetic energy is lost. This means that after colliding with the ground, the ball has 90% of its previous potential energy at the top of its flight. To find the total energy after four bounces, we multiply the initial potential energy by 
The initial potential energy is:
Use our exponential expression to find the remaining energy after four bounces.
Based on conservation of energy, we can find the height that the ball travels with this remaining kinetic energy
Example Question #1 : Conservation Of Energy
A 


The energies involved in this problem are kinetic and potential energy. Conservation of energy shows that the initial energies will be equal to the final energies.
Choosing the bottom of the incline to be the zero height, the ball starts out with kinetic energy and zero potential energy. When the ball reaches maximum height, its velocity is zero (zero kinetic energy). This simplifies our energy equation.
Isolate the height variable and use the given values to solve for the maximum height.
This is the vertical height. The work done by gravity is calculated as the product for force and distance.
The minus sign indicates that the force of gravity acts downward (negative direction).
Example Question #2 : Conservation Of Energy
A roller coaster of mass 500kg is at its highest point in a loop traveling at a velocity of 
More information is needed to solve
This problem covers the conservation of energy (including friction):
The only term we can eliminate is final potential energy:
Expanding each of the terms, we get:
We can rearrange this to solve for final velocity:
Many students will look at this and feel that the equation has just become more complex or harder to follow. However, the idea behind this is to reduce calculation errors. By doing all of your subsitutions of variables and rearrangements of the equations before plugging in your values, you only have to do a single calculation. This greatly reduces the frequency of silly calculation errors. Furthermore, it tends to make it much easier to follow your units in case you need to troubleshoot the problem.
Now, plugging in all of our values, we get:
Example Question #4 : Conservation Of Energy
Consider the following system:
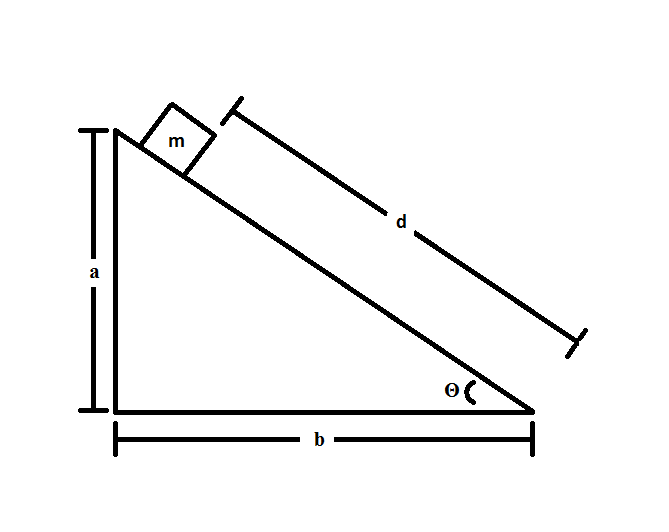
The coefficient of friction between the block and the slope is 



First, we'll write out the equation for conservation of energy:
The velocity of the block is constant, so kinetic energies will cancel out. Furthermore, we can remove final potential energy if we say that the final height is 0m. Therefore, we get:
Substituting in the expression for potential energy, we get:
Note that this problem cannot be solved by using the force of gravity and force of friction because we do not know the angle of the slope.
Example Question #8 : Conservation Of Energy
A pebble is dropped from a height of 

Energy in a system must be conserved, and the energy in the falling pebble is either potential or kinetic:
Potential energy is represented by the 
Kinetic energy is represented by the 
At the exact moment the pebble is released, its stationary, so
Example Question #9 : Conservation Of Energy
Terry believes he can throw a ball vertically and hit a target 

This problem deals with both potential energy and kinetic energy.
Potential energy is expressed as:
Kinetic energy is expressed as:
Energy must be conserved, so set up the following equation:
The initial height can be treated as zero, as can the final velocity. Plug in these zero values into the above equation.
Solve for 

All AP Physics 1 Resources