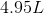We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Chemistry : Stoichiometry

Study concepts, example questions & explanations for AP Chemistry

Create An Account

All AP Chemistry Resources

6 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Stoichiometry

For the molecular formula, $CH_{3}CH_{2}Br$ , how many moles of bromine are in 20.0 grams of this molecule?

Possible Answers:

1.10mol

20.55mol

0.1835mol

8.1112mol

15.0mol

Correct answer:

0.1835mol

Explanation:

The first step is to determine the molecular weight of the molecule:

$MW=(atomic\ weight\ of\ C)+(atomic\ weight\ of\ H)+(atomic\ weight\ of\ Br)$

$MW_{CH_{3}CH_{2}Br}=2(12\frac{g}{mole})+5(1\frac{g}{mole})+(80\frac{g}{mole})=109 \frac{g}{mole}$

The molecular weight serves as a conversion factor to convert grams to moles as implied its units $\frac{g}{mole}$ . So, given that we are dealing with 20.0 grams, the moles of 20.0 grams can be calculated using the calculated molecular weight as seen below in which the grams cancel out leaving the units in moles:

$20.0 g * \frac{mole}{109\ grams} =0.1835\ moles\ CH_{3}CH_{2}Br$

Based on the molecular formula, for every mole of the compound $CH_{3}CH_{2}Br$ , there is 1 mole of bromine. Based on our calculations 20.0 grams of $CH_{3}CH_{2}Br$ is 0.1835 moles of the compound. Because there is a 1:1 molar ratio of bromine to every molecule, we have 0.1835 moles of bromine in 20 grams of our compound, $CH_{3}CH_{2}Br$ .

Report an Error

Example Question #32 : Stoichiometry

For the molecular formula, $CH_{3}CH_{2}OH$ , how many grams of oxygen are in 50.0g of this molecule?

Possible Answers:

17.4g

16.2g

46.1g

12.4g

20.7g

Correct answer:

17.4g

Explanation:

The first step is to determine the molecular weight of the molecule ethanol, $CH_{3}CH_{2}OH$ :

$MW=\text{respective equivalents *[(atomic weight of C)+(atomic weight of H)+(atomic weight of O)]}$

$MW_{CH_{3}CH_{2}OH}=2\left(\frac{12g}{mol}\right)+6\left(\frac{1g}{mol}\right)+\left(\frac{16g}{mol}\right)=46 \frac{g}{mol}$

The molecular weight serves as a conversion factor to convert grams to moles as implied by its units $\frac{grams}{mole}$ . So, given that we are dealing with 50 grams of ethanol, the moles of 50 grams can be calculated using the calculated molecular weight as seen below in which the grams cancel out leaving the units in moles:

$50g * \frac{1mole}{46 g} =1.09 mol\ CH_{3}CH_{2}OH$

Based on the molecular formula, we can see that for every mole of the compound $CH_{3}CH_{2}OH$ , there is 1 mole of oxygen. Based on our calculations, 50 grams of $CH_{3}CH_{2}OH$ is 1.09 moles of the compound. Because there is a 1:1 molar ratio of oxygen to every ethanol molecule, that is, 1 mole of oxygen in every mole of our molecule, we have 1.09 moles of oxygen in 50 grams of our compound $CH_{3}CH_{2}OH$ . To convert 1.09 moles of oxygen to grams of oxygen, we perform the following equation based on the atomic weight of oxygen, which from the periodic table we know is $16\frac{g}{mol}$ :

$1.09 mol * \frac{16g}{mol}= 17.4 g\ oxygen$

Report an Error

Example Question #6 : Other Stoichiometric Calculations

For the molecular formula, $C_{4}H_{9}O_{2}$ , how many grams of oxygen are in 45.0 grams of this molecule?

Possible Answers:

10.1g

25.4g

11.4g

55.0g

16.2g

Correct answer:

16.2g

Explanation:

The first step is to determine the molecular weight of the molecule:

$MW=\text{respective equivalents *[(atomic weight of C)+(atomic weight of H)+(atomic weight of O)]}$

$MW_{C_{4}H_{9}O_{2}}=4(12\frac{g}{mole})+9(1\frac{g}{mole})+2(16\frac{g}{mole})= 89 \frac{g}{mole}$

The molecular weight serves as a conversion factor to convert grams to moles as implied its units $\frac{g}{mole}$ . So, given that we are dealing with 45.0 grams, the moles of 45.0 grams can be calculated using the calculated molecular weight as seen below in which the grams cancel out leaving the units in moles:

$45.0g * \frac{mole}{89.0\ grams} =0.506\ moles C_{4}H_{9}O_{2}$

Based on the molecular formula, we can see that for every mole of the compound $C_{4}H_{9}O_{2}$ , there are 2 moles of oxygen. Based on our calculations 45.0 grams of $C_{4}H_{9}O_{2}$ is 0.506 moles of the compound. Because there is a 2:1 mole ratio of oxygen to every molecule, that is, 2 mole of oxygen in every mole of our molecule, we have double the moles of oxygen in our compound $C_{4}H_{9}O_{2}$ as calculated below:

$0.506\ moles_{C_{4}H_{9}O_{2}} * \frac{2\ moles\ of\ oxygen}{1\ mole_{C_{4}H_{9}O_{2}}}=1.011\ moles\ of\ oxygen$

To convert 1.011 moles of oxygen to grams of oxygen, we perform the following equation based on the atomic weight of oxygen, which is $16\frac{g}{mole}$ :

$1.012\ moles * \frac{16g}{mole}= 16.2 g\ oxygen$

Report an Error

Example Question #1 : Stoichiometry With Reactions

Consider the reaction of baking soda and vinegar in an aqueous solution:

$NaHCO_{3\hspace{1 mm}(s)}+CH_3 COOH_{(l)}\rightarrow CO_{2\hspace{1 mm}(g)}+H_2O_{(l)}+Na^{+}_{(aq)}+CH_3COO^{-}_{(aq)}$

If we begin with 17g of $NaHCO_3$ and excess $CH_3COOH$ , what is the volume of the gas released?

Assume that all gases behave as ideal gases at atmospheric pressure. The temperature is 298K.

Possible Answers:

0.203 L

3.451 L

4.95 L

24.465 L

17.0L

Correct answer:

4.95 L

Explanation:

We begin with 17 g of $NaHCO_3$ , so our first step is to calculate the molecular weight of $NaHCO_3$ .

$\frac{23.0\hspace{1 mm} g\hspace{1 mm}Na}{1\hspace{1 mm}mole\hspace{1 mm}Na}+\frac{1.0\hspace{1 mm}g\hspace{1 mm}H}{1\hspace{1 mm}mole\hspace{1 mm}H}+\frac{12.0\hspace{1 mm}g\hspace{1 mm}C}{1\hspace{1 mm}mole\hspace{1 mm}C}+3\times(\frac{16.0\hspace{1 mm}g\hspace{1 mm}O}{1\hspace{1 mm}mole\hspace{1 mm}O})=\frac{84.0\hspace{1 mm}g\hspace{1 mm}NaHCO_3}{1\hspace{1 mm}mole\hspace{1 mm}NaHCO_3}$

Now with the molecular weight, we will calculate the number of moles within 17 g of $NaHCO_3$ .

$17\hspace{1 mm}g\hspace{1 mm}NaHCO_3\times \frac{1\hspace{1 mm}mole\hspace{1 mm}NaHCO_3}{84.0\hspace{1 mm}g\hspace{1 mm}NaHCO_3}=2.03\times10^{-1}mole\hspace{1 mm}NaHCO_3$

Now we will use this to calculate the number of moles of gas produced. In this reaction, the only gas produced is carbon dioxide.

$2.03\times10^{-1}mole\hspace{1 mm}NaHCO_3\hspace{1 mm}\times\frac{1\hspace{1 mm}mole\hspace{1 mm}CO_2}{1\hspace{1 mm}mole\hspace{1 mm}NaHCO_3}=2.03\times10^{-1}moles\hspace{1 mm}CO_2$

An ideal gas at 1 atmosphere and 298 K has the molar volume of $24.465 \frac{L}{mol}$ .

$2.03\times10^{-1}\hspace{1 mm}mol\hspace{1 mm}CO_2\times \frac{24.465\hspace{1 mm}L\hspace{1 mm}gas}{1\hspace{1 mm}mol\hspace{1 mm}gas}=4.95\hspace{1 mm}L\hspace{1 mm}CO_2$

Report an Error

Example Question #35 : Stoichiometry

What volume of 0.5M NaOH is necessary to neutralize 15mL of 1.0M nitrous acid?

Possible Answers:

10mL

30L

30mL

Correct answer:

30mL

Explanation:

Both the acid and the base provide one equivalent of the necessary ions (H+ and OH–, respectively) and therefore you can use the equation M1V1 = M2V2.

(1)(15) = (0.5)V2

V2 = 30mL

Report an Error

Example Question #2 : Stoichiometry With Reactions

What volume of 0.5M Mg(OH)₂ is necessary to neutralize 15mL of 1.0M nitrous acid?

Possible Answers:

15mL

15L

10mL

30mL

Correct answer:

30mL

Explanation:

This problem is tricky because you must realize that Mg(OH)₂ will release 2 molecules of OH– whenever one dissolves; thus, you only need half the amount of Mg(OH)₂ to neutralize all of the nitrous acid, which only gives 1 equivalent.

M1V1 = M2V2

Plugging in the values, you get 30mL, but in reality you only need half of that amount.

Report an Error

Example Question #3 : Stoichiometry With Reactions

Magnesium will combine with oxygen gas to form magnesium oxide according to the balanced equation below.

$2Mg + O_{2}\rightarrow2MgO$

If 65g of MgO are created in the reaction, how many grams of magnesium are used in the reaction?

Possible Answers:

32.5g

71.2g

25.8g

39.2g

48.6g

Correct answer:

39.2g

Explanation:

In order to determine how many grams of magnesium are used in the reaction, we can use the percentage by mass of magnesium in MgO in order to find out how much magnesium is in 65 grams of MgO. The molar mass of MgO is 40.3 grams. The molar mass of magnesium is 24.3 grams. Dividing 24.3 by 40.3 reveals that magnesium makes up 60% of the mass of MgO.

$\frac{24.3g\ Mg}{40.3g\ MgO}=0.603\sim 60\%$

Multiplying 65 grams by 0.603 reveals that there are 39.2 grams of magnesium in 65 grams of MgO.

$65.0g\ MgO*0.603=39.2g\ Mg$

An alternative means of solving the problem would be to convert grams of MgO to moles. The ratio of MgO to Mg in the given chemical equation is 2:2, thus the number of moles of MgO formed is equal to the number of moles of Mg reacted. Once this number is found, it can be converted back to grams using the molar mass of magnesium.

Report an Error

Example Question #4 : Stoichiometry With Reactions

Consider the following chemical reaction:

$Al_2O_3(s)+3H_2SO_4(aq)\rightarrow Al_2(SO_4)_3(aq)+3H_2O(l)$

How many moles of Al_2(SO_4)_3 will be produced if 75.0mL of water is produced?

Possible Answers:

There is not enough information to answer this question

4.17mol

None of the available answers

1.56 moles

1.39mol

Correct answer:

1.39mol

Explanation:

$75.0\hspace{1 mm}mL\times\frac{1\hspace{1 mm}g\hspace{1 mm}H_2O}{1\hspace{1 mm}mL\hspace{1 mm}H_2O}\times\frac{1\hspace{1 mm}mole\hspace{1 mm}H_2O}{18.0\hspace{1 mm}g\hspace{1 mm}H_2O}\times\frac{1\hspace{1 mm}mole\hspace{1 mm}Al_2(SO_4)_3}{3\hspace{1 mm}moles\hspace{1 mm}H_2O}=1.39\hspace{1 mm}moles\hspace{1 mm}Al_2(SO_4)_3$

This problem is solved based on stoichiometry. Using the molecular weights and ratios in the given reaction, we can solve for the amount of Al_2(SO_4)_3 produced.

Report an Error

Example Question #5 : Stoichiometry With Reactions

The formation of ammonia is given by the following equation:

$3H_2+N_2\rightarrow 2NH_3$

Assuming you started with 20g of hydrogen gas, how much nitrogen gas is necessary to react the hydrogen gas?

Possible Answers:

60g

40g

6.67g

93.33g

Correct answer:

93.33g

Explanation:

We can convert the mass of hydrogen from grams to moles by using the equation moles = mass / molar mass

$\frac{20gH_2}{2\frac{g}{mol}H_2}=10mol H_2$

Now that we have the moles of hydrogen, we can use the molar ratio given in the equation of 1:3. Since we need 1/3 of the moles of hydrogen as nitrogen, we know we need 3.33 moles of nitrogen gas.

$10molH_2*\frac{1molN_2}{3molH_2}=3.33molN_2$

Now, we simply multiply the moles by the molar mass of nitrogen gas (28 grams per mol) and we find we need 93.33 grams of nitrogen gas.

$3.33molN_2*28\frac{g}{mol}N_2=93.33gN_2$

Report an Error

Example Question #6 : Stoichiometry With Reactions

The formation of ammonia is given by the following equation:

$3H_2+N_2\rightarrow 2NH_3$

Assuming you start with 15mol of hydrogen gas, how many moles of nitrogen gas will be needed to completely react the hydrogen gas?

Possible Answers:

15mol

5mol

7.5mol

30mol

45mol

Correct answer:

5mol

Explanation:

Since the amount of hydrogen gas is given in moles, this solution is as easy as using the molar ratio between the reactants. Looking at the equation, we see that there is a 1:3 ratio for nitrogen to hydrogen. As a result, we would need one third of the amount of hydrogen available in order to use up all of the hydrogen gas.

$15mol H_2*\frac{1molN_2}{3mol H_2}=5molN_2$

Report an Error

View AP Chemistry Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View AP Chemistry Tutors

Alexandra
Certified Tutor

Rice University, Bachelor in Arts, Biochemistry and Molecular Biology. University of North Texas Health Science Center, Maste...

View AP Chemistry Tutors

James
Certified Tutor

University of Georgia, Bachelor in Arts, Political Science and Government.

All AP Chemistry Resources

6 Diagnostic Tests 225 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Chicago, Statistics Tutors in San Francisco-Bay Area, Reading Tutors in New York City, GMAT Tutors in Phoenix, French Tutors in Washington DC, Spanish Tutors in San Francisco-Bay Area, LSAT Tutors in Chicago, Spanish Tutors in Phoenix, GRE Tutors in Los Angeles, Physics Tutors in Denver

Popular Courses & Classes

MCAT Courses & Classes in Denver, MCAT Courses & Classes in Philadelphia, SAT Courses & Classes in Atlanta, SSAT Courses & Classes in Atlanta, GMAT Courses & Classes in Atlanta, ISEE Courses & Classes in Washington DC, ACT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Chicago, ACT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Atlanta

Popular Test Prep

GMAT Test Prep in Miami, GMAT Test Prep in Philadelphia, GRE Test Prep in San Francisco-Bay Area, MCAT Test Prep in Phoenix, GRE Test Prep in Atlanta, SSAT Test Prep in Los Angeles, ISEE Test Prep in Houston, ISEE Test Prep in Chicago, MCAT Test Prep in Dallas Fort Worth, GRE Test Prep in San Diego

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Chemistry : Stoichiometry

Study concepts, example questions & explanations for AP Chemistry

All AP Chemistry Resources

Example Questions

Example Question #31 : Stoichiometry

Example Question #32 : Stoichiometry

Example Question #6 : Other Stoichiometric Calculations

Example Question #1 : Stoichiometry With Reactions

Example Question #35 : Stoichiometry

Example Question #2 : Stoichiometry With Reactions

Example Question #3 : Stoichiometry With Reactions

Example Question #4 : Stoichiometry With Reactions

Example Question #5 : Stoichiometry With Reactions

Example Question #6 : Stoichiometry With Reactions

All AP Chemistry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: