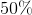For multistep calculations, make sure to keep track of the number of significant figures at the end of each step so we know how many significant figures to round to at the end of the entire calculation. To maintain accuracy, do not round intermediate steps.

First, do the two multiplication problems found within the parentheses.

Recall that for multiplication, the result needs to have the same number of significant figures as the factor with the least number of significant figures. Our answer from the addition should then only have 3 significant figures since that is the number of significant figures 3.14 has. To remember that the answer should only have 3 significant figures, the last significant digit will be highlighted: 

Recall that for multiplication, the result needs to have the same number of significant figures as the factor with the least number of significant figures. Our answer from the addition should then only have 1 significant figure since that is the number of significant figures 10 has. To remember that the answer should only have 1 significant figure, the last significant digit will be highlighted: 

Now, multiply:

Since the factor with the least number of significant figures only has 1 significant figure, the answer must also be rounded to 1 significant figure. 5570.13393 is rounded to 6000.

For multistep calculations, make sure to keep track of the number of significant figures at the end of each step so we know how many significant figures to round to at the end of the entire calculation. To maintain accuracy, do not round intermediate steps.

First, do the two multiplication problems found within the parentheses.

Recall that for multiplication, the result needs to have the same number of significant figures as the factor with the least number of significant figures. Our answer from the addition should then only have 1 significant figure since that is the number of significant figures 0.02 has. To remember that the answer should only have 3 significant figures, the last significant digit will be highlighted: 

Next, do the addition.

Because this is addition, the result of the calculation needs to have the same number of decimal places as the number with the fewest decimal places. We need to only keep 1 decimal place because of . The last significant digit from this step is highlighted: 

Next, do the second addition.

Because this is addition, the result of the calculation needs to have the same number of decimal places as the number with the fewest decimal places. Since 10 does not have any decimal places, our final answer also cannot have any decimal places. 33.356 is rounded down to 33.

To find the percent conversion, use the following equation:

Initially there are 3 mols of . We know that every 1 mol of  that is consumed in the reaction yields 1 mol of . Therefore, the final amount of  in mols is

Plugging this into the above equation gives a conversion rate of 58%.

To find the percent error in your  value, you can use the following equation:

Doing this, we find the percent error to be 4.6%.

When chemists synthesize compounds in the lab, a theoretical yield can be calculated by using knowledge of the full, balanced chemical equation, as well as the starting amounts of all reagents including the limiting reagent. However, due to a variety of factors, the actual yield obtained at the end of the experiment is nearly always going to be lower than the theoretical yield. Some of the things that can cause this are experimental error and side reactions, among others. Thus, chemists usually take the ratio of actual yield to theoretical yield to give the percent yield.

This means that the overall process was  efficient.

The addition of so much salt (NaCl) caused the water to reach its solubility limit for NaCl. This means that no matter how much more NaCl you add to that solution or how hard you stir, it will not dissolve, and will precipitate on the bottom of the beaker. This type of solution is saturated. If the solution were unsaturated, then more salt would still be able to dissolve.

There is no special isotope that makes NaCl insoluble in water. The vigorous mixing would have separated any clumps, and if the solution was unsaturated the salt would have eventually dissolved. Magnesium chloride, another salt, is very soluble in water and would not result in the scenario described.

Each test gives us a different piece of information. The first test tells us that our compound is soluble in water. The second test tells us that heat is released when acid is added. The third test tells us that the solution turns red litmus paper blue, which means that the solution is basic. From these results, we can conclude that the compound is a water-soluble base. Now we can look at our answer options.

, , , and  are all acids.

, however, will generate cyanide ions in solution. Cyanide is basic; thus, this is our correct answer.

The target is precise because the shots are closely grouped together. However, the shots are not accurate because they are not in the middle of the target.

The target is accurate because the shots are all in the middle of the target. It is also precise because all the shots are grouped together.

The shots are not precise because they are not grouped together. However, one of the shots is in the center of the target, and thus is accurate.